
Tính toán cấu kiện chịu uốn theo TTGH2
Mục lục
Mở đầu
Khi thiết kế và tính toán các cấu kiện trong công trình xây dựng, không chỉ cần quan tâm đến khả năng chịu tải và đảm bảo an toàn về cường độ (theo trạng thái giới hạn thứ nhất – TTGH1) (Bạn đọc có thể tham khảo bài blog Tính toán cấu kiện chịu uốn theo TTGH1), mà còn cần đảm bảo các yêu cầu về độ bền, độ cứng và khả năng sử dụng lâu dài của công trình. Điều này được thực hiện thông qua việc kiểm tra theo trạng thái giới hạn thứ hai (TTGH2), đảm bảo cấu kiện không bị biến dạng quá mức, nứt hoặc võng quá lớn trong quá trình sử dụng.
TTGH2 tập trung vào kiểm soát các yếu tố ảnh hưởng đến khả năng sử dụng và hiệu suất của cấu kiện, bao gồm độ võng, độ rung, và khả năng chống nứt. Việc đảm bảo cấu kiện chịu uốn đạt yêu cầu theo TTGH2 là rất quan trọng để tránh các tình trạng làm giảm tuổi thọ hoặc gây ra các vấn đề về thẩm mỹ và an toàn của công trình.
Bài viết này Cemcons sẽ cung cấp hướng dẫn chi tiết về cách tính toán cấu kiện chịu uốn theo TTGH2, từ việc xác định các tiêu chí thiết kế quan trọng đến minh họa các ví dụ thực tế, giúp bạn hiểu rõ cách kiểm soát và đánh giá các yếu tố ảnh hưởng đến khả năng sử dụng của cấu kiện.
Lý thuyết tính toán nứt
Tính toán theo các trạng thái giới hạn thứ hai bao gồm:
- Tính toán theo sự hình thành vết nứt: được tiến hành khi phải đảm bảo không có vết nứt được hình thành, đồng thời cũng cần thiết để bổ sung cho tính toán mở rộng vết nứt và tính toán biến dạng;
- Tính toán theo sự mở rộng vết nứt;
- Tính toán biến dạng (độ võng).
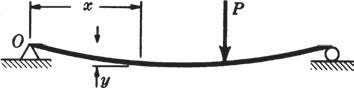

Tính toán Mcr:
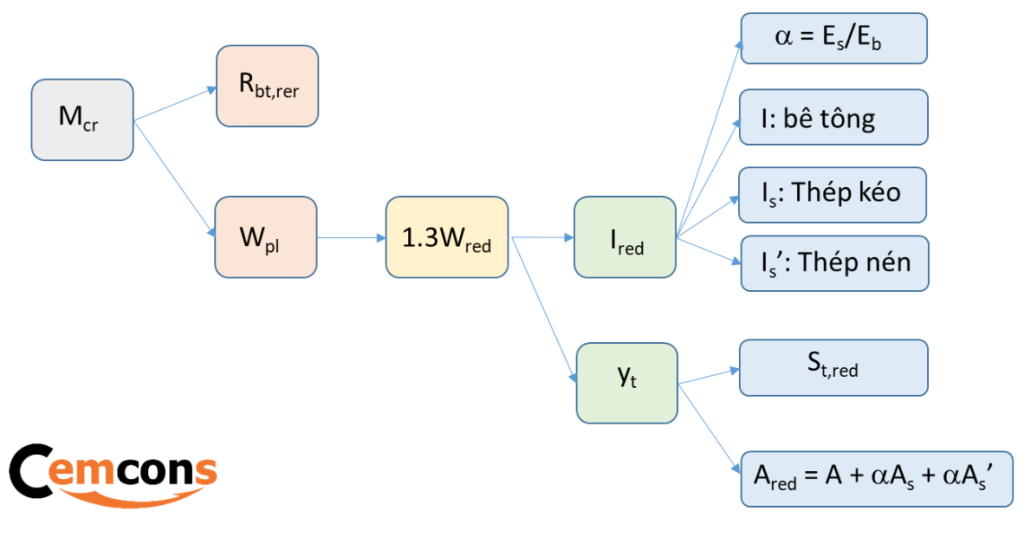
Tính toán yt:
\(y_t\) là khoảng cách từ thớ bê tông chịu kéo nhiều nhất đến trọng tâm tiết diện quy đổi của cấu kiện: \(y_t = \frac{S_{t,red}}{A_{red}}\)
Trong đó:
- \(S_{t, \text{red}}\) là mô men tĩnh của diện tích tiết diện quy đổi của cấu kiện đối với thớ bê tông chịu kéo nhiều hơn.
- \(A_{\text{red}}\) là diện tích của tiết diện ngang quy đổi của cấu kiện, được xác định theo công thức: \(A_{\text{red}} = A + \alpha A_s + \alpha A_s’\)
- \(\alpha\) là hệ số quy đổi cốt thép về bê tông, \(alpha = \frac{E_s}{E_b}\)
- \(A, \, A_s, \, A_s’\) là diện tích tiết diện ngang lần lượt của bê tông, của cốt thép chịu kéo và của cốt thép chịu nén;
Tính toán Wred :
Mô men kháng uốn Wred được xác định theo các công thức: \(W_{\text{red}} = \frac{I_{\text{red}}}{y_t}\)
Trong đó:
- Ired là mô men quán tính của tiết diện quy đổi của cấu kiện đối với trọng tâm của nó:
\(I_{\text{red}} = I + \alpha I_s + \alpha I_s’\)
- \(I, \, I_s, \, I_s’\) là mô men quán tính lần lượt của tiết diện bê tông, của tiết diện cốt thép chịu kéo và của cốt thép chịu nén;
Cho phép xác định mô men kháng uốn Wred mà không kể đến cốt thép.
Tính toán Mcr:
Mô men hình thành vết nứt có kể đến các biến dạng không đàn hồi của vùng bê tông chịu kéo được xác định theo công thức: \(M_{\text{crc}} = W_{\text{pl}} R_{bt, \text{ser}} = 1.3 W_{\text{red}} R_{bt, \text{ser}}\)
Trong đó:
- \(W_{\text{pl}}\) là mô men kháng uốn đàn dẻo của tiết diện đối với thớ bê tông chịu kéo ngoài cùng.
- \(R_{bt, \text{ser}}\) là cường độ chịu kéo tiêu chuẩn của bê tông
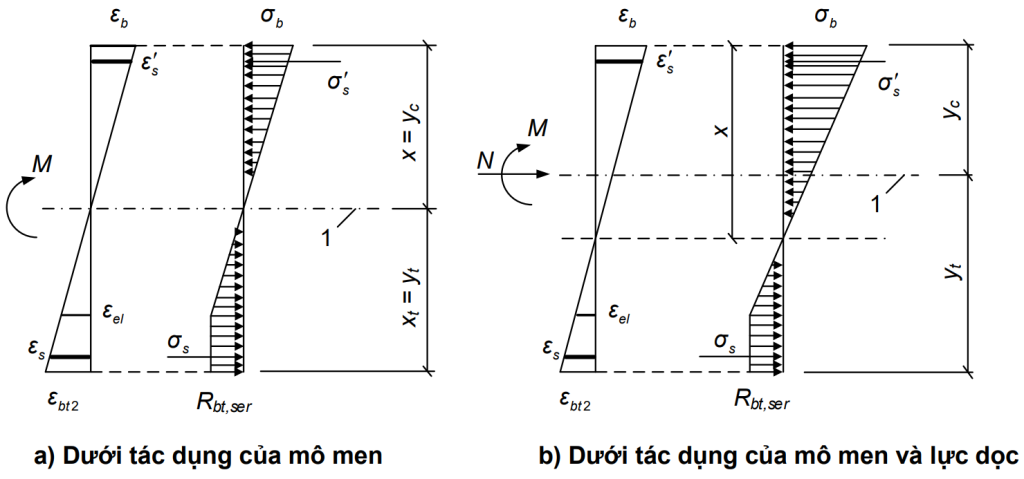
Tính toán theo sự hình thành vết nứt của cấu kiện bê tông cốt thép được tiến hành trong các trường hợp khi mà:
\(M > M_{\text{crc}}\)
Trong đó:
- \(M\) là mô men uốn do ngoại lực đối với trục vuông góc với mặt phẳng tác dụng của mô men uốn và đi qua trọng tâm tiết diện ngang quy đổi của cấu kiện;
- \(M_{\text{crc}}\) là mô men uốn do tiết diện thẳng góc của cấu kiện chịu khi hình thành vết nứt.
Tính toán chiều rộng vết nứt thẳng góc với trục dọc cấu kiện:
\(a_{\text{crc}, i} = \phi_1 \phi_2 \phi_3 \psi_s \frac{\sigma_s}{E_s} L_s \quad (i = 1, 2, 3)\)
Trong đó:
- \(\sigma_s\) là ứng suất trong cốt thép dọc chịu kéo tại tiết diện thẳng góc có vết nứt do ngoại lực tương ứng.
- \(L_s\) là khoảng cách cơ sở giữa các vết nứt thẳng góc kề nhau.
- \(\Psi_s = 1 – 0.8 \frac{M_{\text{crc}}}{M}\) kể đến sự phân bố không đều biến dạng tương đối của thép bị kéo giữa các vết nứt.
- \(\phi_1\) kể đến thời hạn tác dụng của tải trọng, =0 cho tác dụng ngắn hạn; =1.4 cho tác dụng dài hạn.
- \(\phi_2\) kể đến loại hình dạng bề mặt của cốt thép dọc, =5 − thép có gân và cáp; =0.8 − cốt thép trơn.
- \(\phi_3\) là hệ số kể đến đặc điểm chịu lực, =0 − khi chịu uốn và nén lệch tâm; 1.2 − với cấu kiện chịu kéo.
- \(E_s\) là mô đun đàn hồi của cốt thép
Tính toán ứng suất trong cốt thép chịu kéo:
\(\sigma_s\) là ứng suất trong cốt thép dọc chịu kéo tại tiết diện thẳng góc có vết nứt do ngoại lực tương ứng: \(\sigma_s = \frac{M(h_0 – y_c)}{I_{\text{red}}} \alpha_{s1}\)
M: Moment do tải trọng gây ra, h0 là chiều cao làm việc.
\(y_c\): chiều cao vùng nén tiết diện ngang quy đổi
\(x = y_c = h_0 \left( \sqrt{\left( \mu_s \alpha_{s2} + \mu_s’ \alpha_{s1} \right)^2 + 2 \left( \mu_s \alpha_{s2} + \mu_s’ \alpha_{s1} \frac{a’}{h_0} \right)} – \left( \mu_s \alpha_{s2} + \mu_s’ \alpha_{s1} \right) \right)\)
\(\alpha_{s1}, \, \alpha_{s2}\): các hệ số quy đổi thép về bê tông, xác định theo mục 8.2.3.3.2 (TCVN 5574-2018)
\(\alpha_{s1} = \alpha_{s2} = \alpha_s = \frac{E_s}{E_{b, \text{red}}}\)
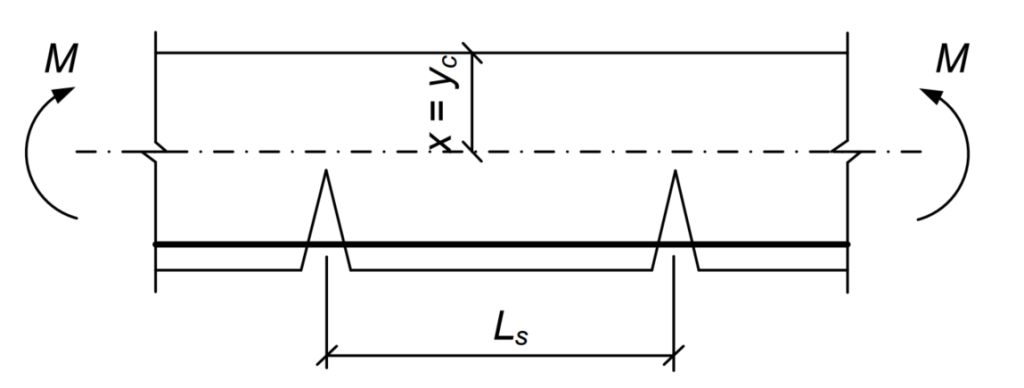
\(E_{b, \text{red}}\): Mô đun biến dạng quy đổi của bê tông chịu nén: \(E_{b, \text{red}} = \frac{R_{b,n}}{\varepsilon_{b1, \text{red}}}\)
\(\varepsilon_{b1, \text{red}}\): Biến dạng tương đối của bê tông lấy bằng 0.0015
\(I_{\text{red}}\): Mô men quán tính vùng chịu nén của tiết diện ngang quy đổi của bê tông:
\(I_{\text{red}} = I_b + I_s \alpha_{s2} + I_s’ \alpha_{s1}\)
\(I_b, \, I_s, \, I_s’\): Mô men quán tính của tiết diện lần lượt vùng bê tông chịu nén, của cốt thép chịu kéo và cốt thép chịu nén đối với trọng tâm tiết diện ngang quy đổi kể đến bê tông vùng chịu kéo.
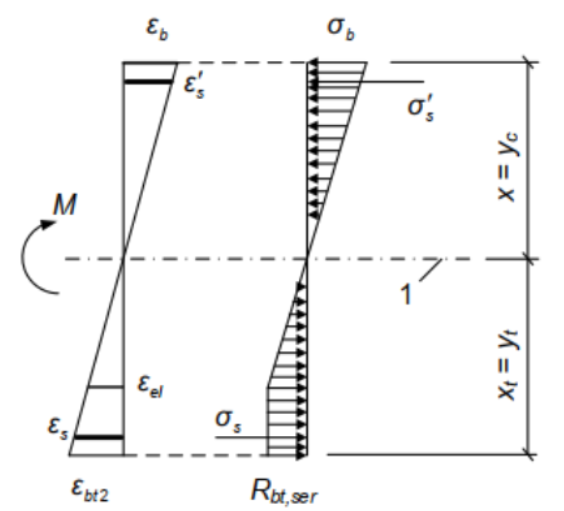
Tính toán khoảng cách cơ sở giữa các vết nứt:
\(L_s\): Khoảng cách cơ sở giữa các vết nứt thẳng góc kề nhau, \(L_s \geq \min(10d_s, 100 \, \text{mm}) \quad \text{and} \quad L_s \leq \min(40d_s, 400 \, \text{mm})\).
\(L_s = \frac{0.5 A_{bt}}{A_s} d_s\)
- Abt: Diện tích tiết diện bê tông chịu kéo, được xác định theo yt.
Trong mọi trường hợp: \(2a \leq y_t \leq 0.5h\)
- As: Diện tích tiết diện cốt thép chịu kéo
ds: Đường kính danh nghĩa của cốt thép \(d_s = \frac{n_1 d_1^2 + n_2 d_2^2 + \cdots + n_k d_k^2}{n_1 d_1 + n_2 d_2 + \cdots + n_k d_k}\).

Kiểm tra chiều rộng vết nứt:
Chiều rộng vết nứt dài hạn được xác định theo công thức:
\(a_{\text{crc}} = a_{\text{crc.1}}\)
còn chiều rộng vết nứt ngắn hạn được xác định theo công thức:
\(a_{\text{crc}} = a_{\text{crc.1}} + a_{\text{crc.2}} – a_{\text{crc.3}}\)
Trong đó:
- \(a_{\text{crc.1}}\) là chiều rộng vết nứt do tác dụng dài hạn của tải trọng thường xuyên và tạm thời dài hạn (0.35LL);
- \(a_{\text{crc.2}}\) là chiều rộng vết nứt do tác dụng ngắn hạn của tải trọng thường xuyên và tạm thời (dài hạn và ngắn hạn);
- \(a_{\text{crc.3}}\) là chiều rộng vết nứt do tác dụng ngắn hạn của tải trọng thường xuyên và tạm thời dài hạn (0.35LL).
Riêng khu vực F lấy \(\Psi = 0.6\), và các trường hợp khác khi có chỉ dẫn cụ thể.
Điều kiện kiểm tra: \(a_{\text{crc}} \leq a_{\text{crc,u}}\)
\(a_{\text{crc}}\): Chiều rộng vết nứt do tác dụng của ngoại lực.
\(a_{\text{crc,u}}\): Chiều rộng vết nứt giới hạn cho phép, Bảng 17
Kiểm tra chiều rộng vết nứt ngắn hạn do tải trọng thường xuyên và tạm thời: \(a_{\text{crc}}^{dh} \leq \left[ a_{\text{crc}}^{dh} \right]\)
- \(a_{\text{crc}}^{nh}\): Chiều vết nứt ngắn hạn: \(a_{\text{crc}}^{nh} = a_{\text{crc,1}} + a_{\text{crc,2}} – a_{\text{crc,3}}\)
- \(\left[ a_{\text{crc}}^{nh} \right]\): Chiều rộng vết nứt nứt giới hạn cho phép ngắn hạn, Bảng 17
Kiểm tra chiều rộng vết nứt dài hạn do tải trọng thường xuyên và tạm thời dài hạn: \(a_{\text{crc}}^{dh} \leq \left[ a_{\text{crc}}^{dh} \right]\)
- \(a_{\text{crc}}^{dh}\): Chiều rộng vết nứt dài hạn: \(a_{\text{crc}}^{dh} = a_{\text{crc,1}}\)
- \(\left[ a_{\text{crc}}^{dh} \right]\): Chiều rộng vết nứt giới hạn cho phép dài hạn, Bảng 17
Bảng 17 – Chiều rộng vết nứt giới hạn cho phép
Loại cốt thép | Tiêu chuẩn | Giá trị acrc,u của vết nứt | |
Dài hạn | Ngắn hạn | ||
1. Theo điều kiện đảm bảo tính toàn vẹn cho cốt thép | |||
CB240-T, CB300-T | TCVN 1651-1:2008 | 0.3 | 0.4 |
CB300-V, CB400-V, CB500-V | TCVN 1651-2:2008 | ||
Dây thép vuốt nguội | TCVN 6288:1997 | ||
Cốt thép thanh cường độ cao (có giới hạn chảy quy ước 835, 930 và 1 080 MPa) | TCVN 6284-5:1997 | 0.2 | 0.3 |
Dây thép kéo nguội cường độ cao | TCVN 6284-2:1997 | ||
Cáp 7 sợi đường kính 12.4 mm trở lên | TCVN 6284-4:1997 | ||
Cáp 19 sợi | |||
Cáp 7 sợi đường kính nhỏ hơn 12.4 mm | TCVN 6284-4:1997 | 0.1 | 0.2 |
2. Theo điều kiện hạn chế thấm cho kết cấu | |||
| – | 0.2 | 0.3 |
Ví dụ tính toán nứt
Đề bài: Sử dụng thông số của cấu kiện dầm ở bài Blog tính toán cấu kiện chịu uốn theo TTGH1 để tiến hành tính toán theo TTGH2. Giả sử tải trọng tiêu chuẩn bằng với tải trọng tính toán và nhịp dầm Ld = 7800 (mm)
Kiểm tra sự hình thành vết nứt
Kiểm tra sự hình thành khe nứt dầm theo TTGH II được tính toán theo 8.2.2.2 TCVN 5574:2018.
Các đặc trưng hình học
Hệ số quy đổi diện tích thép về diện tích bê tông tương đương:
\(\alpha = \frac{E_s}{E_b} = \frac{200000}{30000} = 6.67\)
Diện tích mặt cắt ngang tiết diện dầm:
\(A = b h = 250 \times 600 = 150000 \, (\text{mm}^2)\)
Diện tích mặt cắt ngang quy đổi của tiết diện dầm:
\(A_{\text{red}} = A + \alpha \left( A_s + A_s’ \right) = 150000 + 6.67 \times \left( 1658.72 + 307.87 \right) = 163400.35 \, (\text{mm}^2)\)
Moment tĩnh của tiết diện quy đổi đối với thớ bê tông chịu kéo:
\(S_{\text{t,red}} = \frac{b h^2}{2} + \alpha \left( A_s a + A_s’ (h – a’) \right) = \frac{250 \times (550.83)^2}{2} + 6.67 \times \left( 1658.72 \times 45.43 + 307.87 \times (600 – 32) \right) = 46724291.5 \, (\text{mm}^3)\)
Khoảng cách từ thớ bê tông chịu kéo nhiều nhất đến trọng tâm tiết diện quy đổi:
\(y_t = \frac{S_{\text{t,red}}}{A_{\text{red}}} = \frac{46724291.5}{163400.35} = 285.95 \, (\text{mm})\)
Momen quán tính quy đổi của tiết diện đối với trọng tâm của nó:
\(I_{\text{red}} = I + \alpha I_s + \alpha I_s’ = \frac{b h^3}{12} + \alpha A_s (y_t – a)^2 + \alpha A_s’ (h – y_t – a’)^2 = 4037043926.11 \, \text{mm}^4\)
Momen kháng uốn của tiết diện quy đổi:
\(W_{\text{red}} = \frac{I_{\text{red}}}{y_t} = \frac{4037043926.11}{285.95} = 18540459.71 \, \text{mm}^3\)
Momen hình thành khe nứt
Momen kháng uốn đàn hồi dèo của tiết diện đối với thớ bê tông chịu kéo ngoài cùng:
\(W_{\text{pl}} = \gamma W_{\text{red}} = 1.3 \times 18540459.71 = 24102597.62 \, \text{mm}^3\)
Với \(\gamma = 1.3\) lấy đối với tiết diện chữ nhật.
Momen hình thành khe nứt:
\(M_{\text{crc}} = W_{\text{pl}} \cdot R_{\text{bt,ser}} = 24102597.62 \times 1.55 \times 10^{-6} = 37.35 \, \text{kNm}\)
Kiểm tra: \(M = 250 \, \text{kNm} > M_{\text{crc}} = 37.35 \, \text{kNm}\). Vậy dầm hình thành khe nứt tại nhịp, tính toán bề rộng khe nứt trong trường hợp dầm hình thành vết nứt.
- Dự báo bề rộng vết nứt
Tiến hành dự báo và kiểm tra bề rộng khe nứt giới hạn trong trường hợp dầm hình thành khe nứt được tính toán theo 8.2.2.3 TCVN 5574:2018.
Biến dạng tương đối giới hạn đàn hồi của bê tông vùng nén: \(\epsilon_{\text{bl,red}} = 0.0015\)
Mô đun biên dạng tương đối của bê tông:
\(E_{\text{b,red}} = \frac{R_{\text{b,ser}}}{\epsilon_{\text{bl,red}}} = \frac{18.5}{0.0015} = 12333.33 \, \text{MPa}\)
Giá trị hệ số quy đổi cốt thép về bê tông: \(\alpha_{\text{sl}} = \frac{E_s}{E_{\text{b,red}}} = \frac{200000}{12333.33} = 16.22\)
Hàm lượng cốt thép vùng kéo và nén: \(\mu_s = 1.2\%, \quad \mu_s’ = 0.45\%\)
Chiều cao vùng bê tông chịu nén trung bình của tiết diện ngang quy đổi:
\(y_c = x = h_0 \left[ \sqrt{\alpha_{sl}^2 (\mu_s + \mu_s’)^2 + 2 \alpha_{sl} \left( \mu_s + \mu_s’ \frac{a’}{h_0} \right)} – \alpha_{sl} (\mu_s + \mu_s’) \right] = 236.86 \, \text{mm}\)
Momen quán tính của cấu kiện có kể đến diện tích của vùng bê tông chịu nén, cốt thép chịu kéo, cốt thép chịu nén:
\(I_{\text{red}} = I + \alpha I_s + \alpha I_s’ = \frac{b h^3}{12} + \alpha A_s (y_t – a)^2 + \alpha A_s’ (h – y_t – a’)^2 = 4037043926.11 \, \text{mm}^4\)
Giá trị ứng suất trong cốt thép chịu kéo:
\(\sigma_s = \frac{M (h_0 – y_c)}{I_{\text{red}}} \quad \alpha_{\text{sl}} = 315.37 \, \text{MPa}\)
Diện tích tiết diện bê tông chịu kéo:
\(A_{\text{bt}} = b \cdot y_t = 300 \times 285.95 = 85785 \, \text{mm}^2\)
Khoảng cách cơ sở giữa các khe nứt thẳng góc kề nhau:
\(L_s = \frac{0.5 \cdot A_{\text{bt}}}{A_s} \cdot d_s = \frac{0.5 \times 85785}{1658.723 \times 20} = 517 \, \text{mm} > 400 \, \text{mm}, \, L_s = 400 \, \text{mm}\)
Bề rộng khe nứt thẳng góc:
\(a_{\text{crc}} = \phi_1 \phi_2 \phi_3 \psi_s \frac{\sigma_s}{E_s} L_s = 1 \times 0.5 \times 1 \times 0.88 \times \frac{315.4}{20000} \times 400 = 1.39 \, \text{mm}\)
Trong đó: giá trị các hệ số lần lượt là: \(\phi_1 = 1\) đối với tải trọng ngắn hạn, \(\phi_2 = 0.5\) đối với thép có gờ và \(\phi_3 = 1.2\) đối với cấu kiện chịu kéo.
Hệ số: \(\psi_s = 1 – 0.8 \times \frac{M_{crc}}{M} = 1 – 0.8 \times \frac{37.35}{250} = 0.88\)
Lý thuyết tính toán võng
Mối quan hệ giữa độ cong và độ võng:
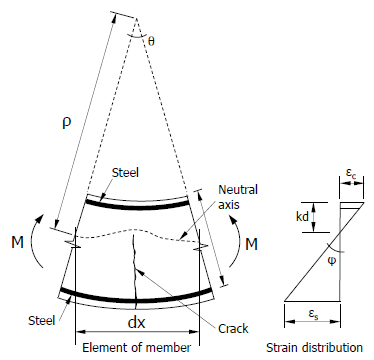
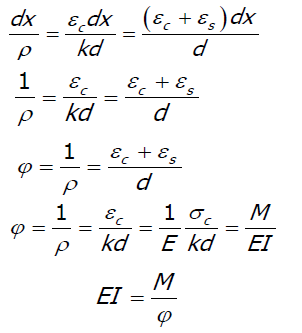
Tính toán độ cong cho một tiết diện cho trường hợp có xảy ra vết nứt:
\(\frac{1}{r} = \frac{1}{r_1} – \frac{1}{r_2} + \frac{1}{r_3}\)
Trong đó:
- \(\left( \frac{1}{r} \right)_1\)là độ cong do tác dụng ngắn hạn của tải trọng thường xuyên và tải trọng tạm thời TT + HT.
- \(\left( \frac{1}{r} \right)_2\) là độ cong do tác dụng ngắn hạn của tải trọng thường xuyên và tải trọng tạm thời dài hạn TT + \(\Psi\)HT.
- \(\left( \frac{1}{r} \right)_3\) là độ cong do tác dụng dài hạn của tải trọng thường xuyên và tải trọng tạm thời dài hạn TT + \(\Psi\)HT.
Theo TCVN 2737-2023 thành phần dài hạn của hoạt tải tạm thời ngắn hạn chiếm phần tải trọng tại thời ngắn hạn.
Riêng khu vực F lấy \(\Psi = 0.35\), và các trường hợp khác khi có chỉ dẫn cụ thể.
Độ cong của 1 tiết diện dưới tác dụng của momen tương ứng xác định theo công thức:
\(\left( \frac{1}{r} \right)_i = \frac{M_i}{D}\)
Trong đó:
- Mi là momen tương ứng.
- D là độ cứng của tiết diện: \(D = E_{b1} \cdot I_{\text{red}}\)
- \(E_{b1}\) là modul biến dạng của bê tông chịu nén, phụ thuộc vào thời hạn tác dụng của tải trọng:
\(E_{b1} = E_{b,\text{red}} = \frac{R_{b,\text{ser}}}{\varepsilon_{b1,\text{red}}}\)
\(\varepsilon_{b1,\text{red}}\) là biến dạng tương đối của bê tông theo Bảng 9 và mục 6.1.4.3
- \(I_{\text{red}}\) xác định tương tự toán bề rộng vết nứt, các hệ số quy đổi cốt thép được xác định như sau:
\(\alpha_{s1} = \frac{E_s}{E_{b,\text{red}}} ; \quad \alpha_{s2} = \frac{E_{s,\text{red}}}{E_{b,\text{red}}}\) với \(E_{s,\text{red}} = \frac{E_s}{\Psi_s}, \quad \Psi_s = 1 – 0.8 \frac{M_{\text{crc}}}{M}\)
\(I_{\text{red}} = b \cdot \frac{y_c^3}{12} + b \cdot y_c \left( \frac{y_c}{2} \right)^2 + A_s \alpha_{s2} (h_0 – y_c)^2 + A_s’ \alpha_{s1} (y_c – a_0′)^2\)
Nhận xét: \(\alpha_{s1}\) và \(\alpha_{s2}\) sẽ khác nhau cho trường hợp dài hạn và ngắn hạn do hệ số \(\varepsilon_{b1,\text{red}}\) khác nhau.
Tính toán độ cong cho một tiết diện cho trường hợp không xảy ra vết nứt:
Độ cong của tiết diện xác định theo công thức:
\(\frac{1}{r} = \frac{1}{r_1} + \frac{1}{r_2}\)
Trong đó:
- \(\frac{1}{r_1}\) là độ cong do tác dụng ngắn hạn của tải trọng tạm thời ngắn hạn (1- )HT.
- \(\frac{1}{r_2}\) là độ cong do tác dụng dài hạn của tải trọng thường xuyên và tải trọng tạm thời dài hạn TT + HT.
- \(\Psi = 0.35\) theo TCVN 2737-2023
Riêng khu vực F lấy \(\Psi = 0.6\), và các trường hợp khác khi có chỉ dẫn cụ thể.
Độ cong của 1 tiết diện dưới tác dụng của momen tương ứng xác định theo công thức:
\(\frac{1}{r_i} = \frac{M_i}{D}\)
Trong đó:
- \(M_i\) là momen tương ứng.
- \(D\) là độ cứng của tiết diện xác định theo công thức: \(D = E_{b1} \cdot I_{\text{red}}\)
- \(E_{b1}\) là modul biến dạng của bê tông chịu nén được xác định phụ thuộc vào thời hạn tác dụng của tải trọng
\(E_{b1} = 0.85 E_b\) (Khi có tác dụng ngắn hạn của tải trọng)
\(E_{b1} = E_{b,\tau} = \frac{E_b}{(1 + \varphi_{b,cr})}\) (Khi có tác dụng của tải dài hạn)
\(\varphi_{b,\text{cr}}\) hệ số từ biến của bê tông tra theo Bảng 11 TCVN 5574:2018.
- Ired xác định tương tự toán bề rộng vết nứt, các hệ số quy đổi cốt thép được xác định như sau:
\(\alpha_{s1} = \frac{E_s}{E_{b,\text{red}}}; \quad \alpha_{s2} = \frac{E_{s,\text{red}}}{E_{b,\text{red}}}\) với \(E_{s,\text{red}} = \frac{E_s}{\Psi_s}\)
\(I_{\text{red}} = \frac{b h^3}{12} + b h \left( \frac{h}{2} – y_t \right)^2 + A_s \alpha_{s2} (h_0 – y_t)^2 + A_s’ \alpha_{s1} (y_t – a_0′)^2\)
Bảng 11 – Hệ số từ biến của bê tông \(\varphi_{b,\text{cr}}\)
Độ ẩm tương đối của không khí môi trường xung quanh, % | Giá trị của φb,cr khi cấp độ bền chịu nén của bê tông nặng bằng | ||||||||||
В10 | В15 | В20 | В25 | В30 | В35 | В40 | В45 | В50 | В55 | В60 đến B100 | |
Trên 75 | 2.8 | 2.4 | 2.0 | 1.8 | 1.6 | 1.5 | 1.4 | 1.3 | 1.2 | 1.1 | 1.0 |
Từ 40 đến 75 | 3.9 | 3.4 | 2.8 | 2.5 | 2.3 | 2.1 | 1.9 | 1.8 | 1.6 | 1.5 | 1.4 |
Dưới 40 | 5,6 | 4.8 | 4.0 | 3.6 | 3.2 | 3.0 | 2.8 | 2.6 | 2.4 | 2.2 | 2.0 |
CHÚ THÍCH: Độ ẩm tương đối của không khí môi trường xung quanh lấy theo độ ẩm tương đối trung bình tháng của tháng nóng nhất đối với vùng xây dựng theo quy định hiện hành. | |||||||||||
Tính toán độ võng của dầm:
Sau khi xác định được tại tiết diện có momen lớn nhất có đảm bảo điều kiện hình thành vết nứt hay không từ đó xác định được độ cong của tiết diện. Từ đó dựa vào công thức dưới đây để xác định độ cong của tiết diện dầm.
\(f = s L_2 \left( \frac{1}{r} \right)_{\text{max}}\)
Trong đó:
- s là hệ số lấy bằng:
- s= 5/48 với dầm tựa tự do
- s= 1/4 với dầm consol.
- L là nhịp của dầm.
- \(\left( \frac{1}{r} \right)_{\text{max}}\) là độ cong toàn phần tại tiết diện có momen uốn lớn nhất.
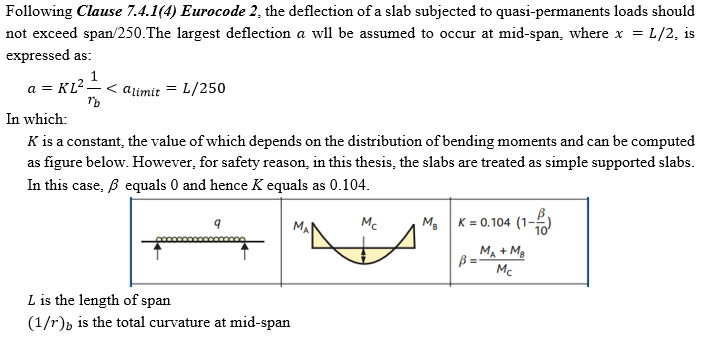
Bảng M1- Độ võng giới hạn theo phương đứng fu
Cấu kiện kết cấu | Các yêu cầu | Độ võng giới hạn theo phương đứng fu | Tải trọng để xác định độ |
1. Dầm cầu trục dưới cần trục kiểu cầu ( cầu trục ) và cần trục treo được điều khiển: | |||
– từ dưới nền , kể cả palăng | Công nghệ | L / 250 | Tải trọng do một cần trục |
– từ cabin ứng với chế độ làm việc ( theo TCVN 8590–1 : 2010 ( ISO 4301-1 : 1986 ) ) | Tâm sinh lý |
|
|
nhóm A1 đến A6 | L / 400 | Tải trọng do một cần trục | |
nhóm A7 | L / 500 | Tải trọng do một cần trục | |
nhóm A8 | L / 600 | Tải trọng do một cần trục | |
2. Dầm , giàn , xà , bản , xà gồ , tầm ( bao gồm cả sườn của tắm và bản ) của: | |||
a ) Mái và sàn tầng nhìn thấy được với nhịp L , m: | Thẩm mỹ – tâm lý |
| Tải trọng thường xuyên và tạm thời dài hạn |
L ≤ 1 | L / 120 | ||
L = 3 | L / 150 | ||
L = 6 | L / 200 | ||
L = 24 ( 12 ) | L / 250 | ||
L ≥ 36 ( 24 ) | L / 300 | ||
Ví dụ tính toán võng
Tính toán độ võng dầm
Tính toán võng cho dầm trong trường hợp hình thành khe nứt được thực hiện theo 8.2.3.2 TCVN 5574:2018
Hệ số kể đến sự phân bố không đều của biến dạng cốt thép vùng kéo giữa các khe nứt:
\(\psi_s = 1 – 0.8 \times \frac{M_{crc}}{M_{tc}} = 1 – 0.8 \times \frac{37.35}{200} = 0.85\)
Mô đun biến dạng quy đổi của cốt thép vùng kéo có xét đến ảnh hưởng của sự làm việc của bê tông vùng kéo giữa các khe nứt:
\(E_{s,red} = \frac{E_s}{\psi_s} = \frac{200000}{0.88} = 227272.73 \, \text{MPa}\)
Hệ số quy đổi của cốt thép vùng nén và vùng kéo:
- Tải tác dụng ngắn hạn:
\(\varepsilon_{b1,red} = 0.0024 \quad \Rightarrow \quad E_{b,red} = \frac{R_{b,ser}}{\varepsilon_{b1,red}} = \frac{22}{0.0024} = 9166.67 \, \text{MPa}\)
\(\alpha_{s1} = \frac{E_s}{E_{b,red}} = \frac{200000}{9166.67} = 21.82\)
\(\alpha_{s2} = \frac{E_{s,red}}{E_{b,red}} = \frac{227272.73}{9166.67} = 24.79\)
- Tải tác dụng dài hạn: (độ ẩm 40% – 70%):
\(\epsilon_{b1,red} = 0.0015 \quad \Rightarrow \quad E_{b,red} = \frac{R_{b,ser}}{\epsilon_{b1,red}} = \frac{22}{0.0015} = 14666.67 \, \text{MPa}\)
\(\alpha_{s1} = \frac{E_s}{E_{b,red}} = \frac{200000}{14666.67} = 13.64\)
\(\alpha_{s2} = \frac{E_{s,red}}{E_{b,red}} = \frac{227272.73}{14666.67} = 15.5\)
Chiều cao vùng nén của bê tông
- Tải tác dụng ngắn hạn
\(y_c = x_m = h_0 \left[ \sqrt{ \left( \mu_s \alpha_{s2} + \mu_s’ \alpha_{s1} \right)^2 + \left( \mu_s \alpha_{s2} + \mu_s’ \alpha_{s1} \frac{a’}{h_0} \right) } – \left( \mu_s \alpha_{s2} + \mu_s’ \alpha_{s1} \right) \right] = 255.61 \, \text{mm}\)
- Tải tác dụng dài hạn
\(y_c = x_m = h_0 \left[ \sqrt{ \left( \mu_s \alpha_{s2} + \mu_s’ \alpha_{s1} \right)^2 + \left( \mu_s \alpha_{s2} + \mu_s’ \alpha_{s1} \frac{a’}{h_0} \right) } – \left( \mu_s \alpha_{s2} + \mu_s’ \alpha_{s1} \right) \right] = 152.06 \, \text{mm}\)
Độ cứng chống uốn của tiến diện ngang quy đổi trong đoạn có khe nứt
- Tải tác dụng ngắn hạn:
\(D_m = E_{b,red} I_{red,m} = 5.39 \times 10^{13} \, \text{Nm}^2\)
- Tải tác dụng dài hạn:
\(D_m = E_{b,red} I_{red,m} = 14.45 \times 10^{13} \, \text{Nm}^2\)
Độ cong toàn phần của sàn trong trường hợp xuất hiện khe nứt
- Độ cong do tác dụng ngắn hạn của toàn bộ tải trọng:
\(\left( \frac{1}{r} \right)_1 = \frac{M}{D_m} = \frac{250 \times 10^6}{5.39 \times 10^{13}} = 4.63 \times 10^{-6} \, \left( \frac{1}{\text{mm}} \right)\)
- Độ cong do tác dụng ngắn hạn của tải trọng thường xuyên và tạm thời dài hạn:
\(\left( \frac{1}{r} \right)_2 = \frac{M}{D_m} = \frac{20.33 \times 10^6}{5.39 \times 10^{13}} = 3.77 \times 10^{-7} \, \left( \frac{1}{\text{mm}} \right)\)
- Độ cong do tác dụng dài hạn của tải trọng thường xuyên và tạm thời dài hạn:
\(\left( \frac{1}{r} \right)_3 = \frac{M}{D_m} = \frac{20.33 \times 10^6}{14.45 \times 10^{13}} = 1.4 \times 10^{-7} \, \text{(1/mm)}\)
- Độ cong toàn phần của dầm:
\(\frac{1}{r} = \left( \frac{1}{r} \right)_1 – \left( \frac{1}{r} \right)_2 + \left( \frac{1}{r} \right)_3 = 4.39 \times 10^{-6} \, \left( \frac{1}{\text{mm}} \right)\)
- Độ võng của dầm:
\(f = s L^2 \left( \frac{1}{r} \right) = \frac{5}{48} \times 7800^2 \times 4.39 \times 10^{-6} = 27.82 \, \text{mm}\)
Trong đó: \(s = \frac{5}{48}\) là hệ số phụ thuộc sơ đồ tính toán.
Tài liệu tham khảo
- Slide thầy Nguyễn Minh Long trường ĐH Bách Khoa TP.HCM
- Tiêu chuẩn TCVN 2737-2023
- Tiêu chuẩn TCVN 5574-2018
- Tiêu chuẩn Eurocode 2
- Thiết kế bê tông cốt thép theo TCVN 5574-2018, thầy Bùi Quốc Bảo
- Hướng dẫn tính toán cấu kiện bê tông cốt thép theo tiêu chuẩn TCVN 5574-2018, cô Đoàn Thị Quỳnh Mai và cộng sự
Link Cemapp Tính toán và thiết kế dầm BTCT hàng loạt theo TCVN 5574:2018
Bạn đọc tham khảo khóa học Hướng dẫn đồ án tốt nghiệp thiết kế nhà cao tầng theo TCVN mới nhất
Khóa học Hướng dẫn đồ án tốt nghiệp ngành Xây dựng theo tiêu chuẩn Eurocodes
Like và share nếu thấy bổ ích <3
Bài viết gần đây


Chia dải strip 1m 2m ảnh hưởng tới nội lực như thế nào?


Bí quyết học tập để được điểm cao cho sinh viên năm 1




