Tính toán cột chịu nén lệch tâm xiên
Mục lục
Mở đầu
Trong thiết kế kết cấu, cột chịu nén lệch tâm xiên là một bài toán phức tạp thường gặp, đòi hỏi sự hiểu biết sâu sắc về cơ học vật liệu và các nguyên lý thiết kế kết cấu. Đây là dạng chịu lực mà cột không chỉ chịu lực nén dọc trục mà còn chịu mô-men lệch tâm theo hai phương, gây ra ứng suất phức hợp trên tiết diện.
Việc tính toán chính xác cho cột chịu nén lệch tâm xiên là vô cùng quan trọng, bởi nó ảnh hưởng trực tiếp đến khả năng chịu tải, độ ổn định, và an toàn của công trình. Các sai sót trong phân tích và thiết kế có thể dẫn đến nguy cơ mất ổn định hoặc phá hủy cột dưới tải trọng thực tế.
Trong bài viết này, Cemcons sẽ giới thiệu cho các bạn cách tính toán cột chịu nén lệch tâm xiên.
Giới thiệu
Chức năng: Cột là một phần quan trọng trong hệ thống kết cấu của một công trình xây dựng. Chúng chịu trách nhiệm truyền tải trọng từ các phần trên xuống nền đất hoặc sàn dưới. Điều này giúp đảm bảo tính ổn định và an toàn cho công trình.
Lịch sử: Cột có một lịch sử lâu đời. Các nền văn minh cổ đại như Ai Cập cổ đại và Hy Lạp cổ đại đã sử dụng cột trong kiến trúc của họ.
Vật liệu sử dụng: Loại vật liệu sử dụng để làm cột cũng đã thay đổi theo thời gian. Trong thời kỳ cổ đại, đá và gỗ thường được sử dụng. Trong thời kỳ hiện đại, bê tông cốt thép và thép là những vật liệu phổ biến cho cột, vì chúng có khả năng chịu lực tốt.

Nguyên lý thiết kế: Theo nguyên tắc cột khỏe dầm yếu vì cột là cấu kiện quan trọng nhất trong phần khung, nếu cột bị phá hoại, hệ sẽ biến hình làm phá hoại toàn bộ công trình.
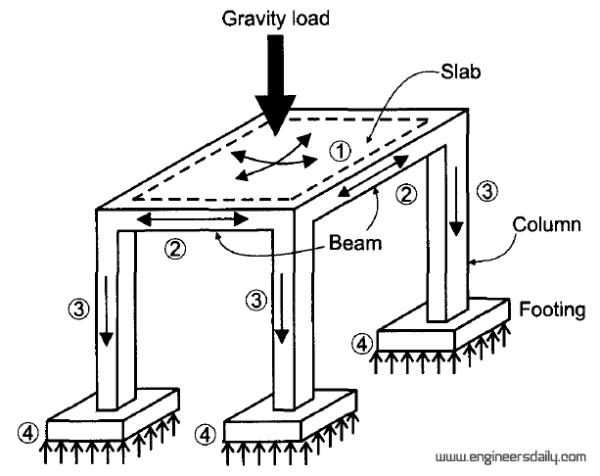

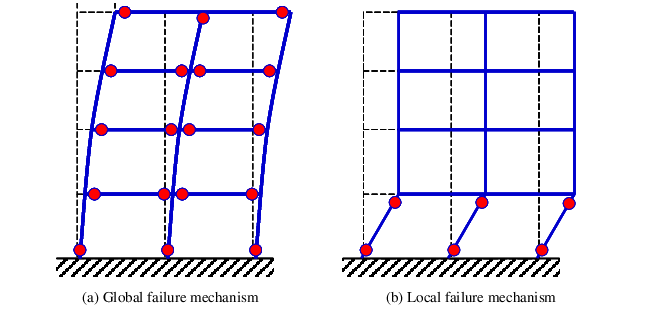
Cấu kiện chịu nén: là cấu kiện chịu tác dụng của lực nén theo phương dọc trục của cấu kiện. Cấu kiện chịu nén lệch tâm: khi lực nén N đặt lệch so với trọng tâm của tiết diện ngang, hay lực N đặt đúng tâm và một moment do tải ngang gây ra.
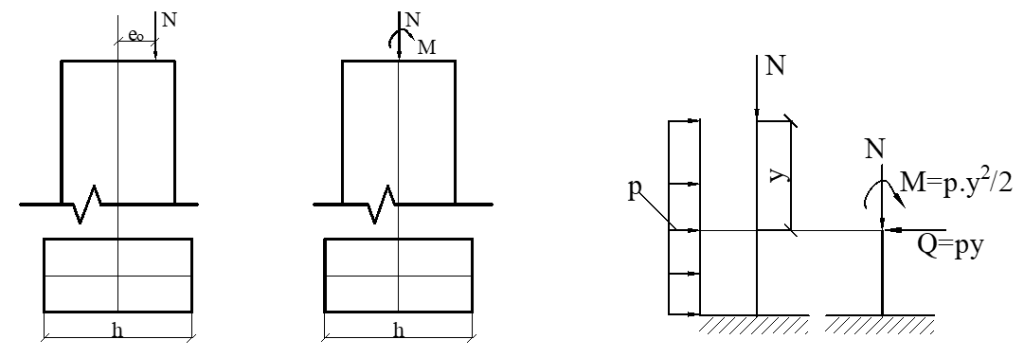
Phân loại cột:
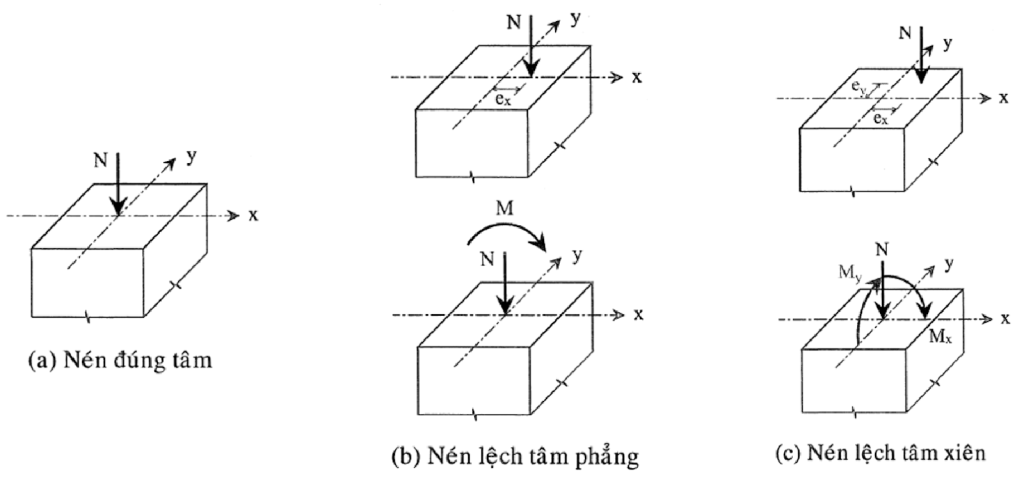
Trong thiết kế cột được chia làm 3 loại:
- Nén đúng tâm: Khi cột chỉ chịu lực dọc và tác dụng đúng tâm
- Nén lệch tâm phẳng: Cột chịu lực dọc và moment theo một phương X hoặc Y
- Nén lệch tâm xiên (phổ biến): Cột chịu lực dọc và moment theo 2 phương X và Y
Phân loại phá hoại cột:


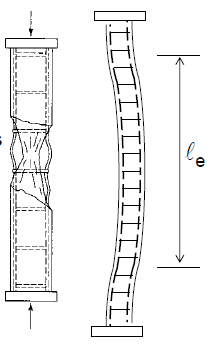
Dựa vào chiều cao và kích thước tiết diện cột được chia làm 2 loại chủ yếu: Cột ngắn và cột mảnh.
Khi cột chịu quá tải có thể dẫn tới:
- Bị vỡ ra do lực nén
- Bị phá hoại do mất ổn định (buckling)
- Tổ hợp của 2 loại phá hoại trên
Cột ngắn thường bị phá hoại bởi lực nén dẫn tới bị vỡ ra do bê tông và cốt thép đạt trạng thới giới hạn
Cột mảnh thường bị phá hoại mất ổn định do chuyển vị ngang của cột. Chuyển vị này gây thêm moment do lực dọc tác động.
Kích thước tiết diện của cột phải:
- Thuận tiện thi công: bxh chọn chẵn 50mm
- Đảm bảo khả năng chịu lực: tính toán và kiểm tra theo TTGH1
- Đảm bảo điều kiện ổn định: \(\lambda \leq \lambda_{\text{gh}}\)
Trong đó:
\(\lambda = \frac{L_0}{i}\) là độ mảnh của cấu kiện
\(L_0 = \psi L\) là chiều dài tính toán
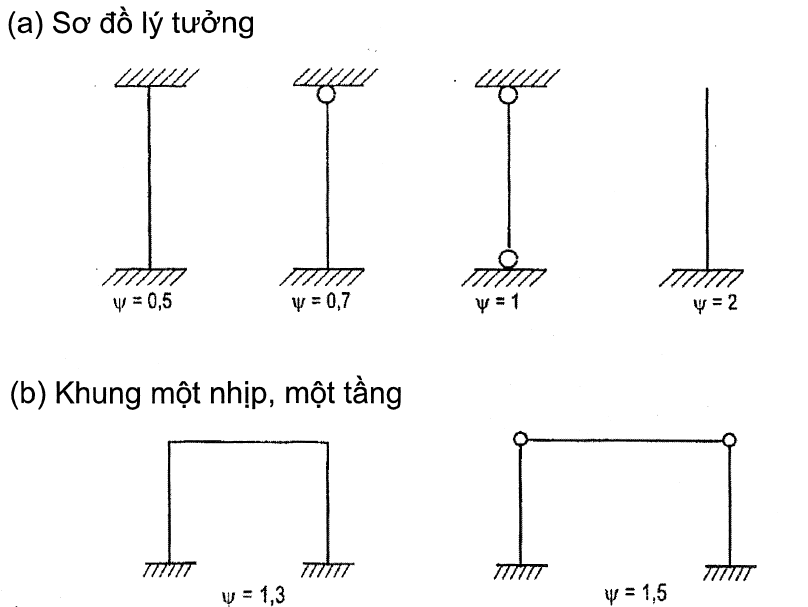
\(\Psi\) là hệ số phaụ thuộc vào sơ đồ liên kết của cấu kiện
L là chiều dài thực tế (chiều cao hình học của cấu kiện)
i là bán kính quán tính, \(i = \sqrt{\frac{I}{A}} = 0.288b\)
\(\lambda_{\text{gh}}\) là độ mảnh giới hạn (cột nhà \(\lambda_{\text{gh}}\) =120, cấu kiện khác \(\lambda_{\text{gh}}\) =200)
Cách tính hệ số phụ thuộc vào sơ đồ liên kết của cấu kiện:

Nội lực tính toán
Nội lực nguy hiểm nhất khi tính toán cột:
Nội lực để tính toán nén lệch tâm xiên được lấy từ kết quả tổ hợp trong đó cần chú ý đến lực dọc, moment phương X, và moment phương Y:
- Có N lớn nhất và Mx, My tương ứng;
- Có Mx lớn nhất, N, My tương ứng;
- Có My lớn nhất, N, Mx tương ứng;
- Có Mx và My đều lớn;
- Có độ lệch tâm ban đầu: \(e_{1x} = \frac{M_x}{N}\) hoặc \(e_{1y} = \frac{M_y}{N}\) lớn.
Trình tự tính toán
Nén lệch tâm xiên xảy ra khi mặt phẳng tác dụng của mô men uốn M không chứa trục đối xứng của tiết diện. Có thể phân tích mô men M thành 2 thành phần tác dụng trong mặt phẳng chứa 2 trục đối xứng của tiết diện (Ox và Oy) là Mx và My. Với góc giữa mặt phẳng uốn và trục Ox là φ0.
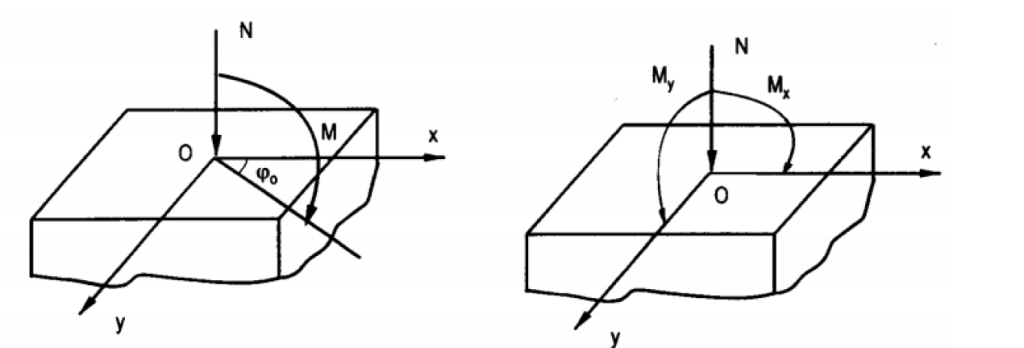
Quy ước chiều moment và kích thước tiết diện:
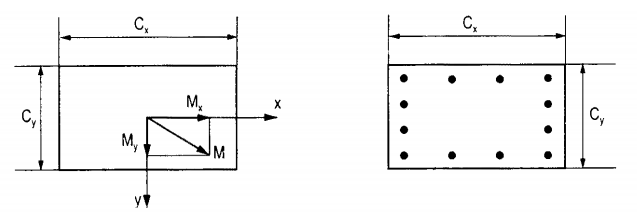
Quy ước phương chiều sách thầy Cống:
- Mx quay quanh trục Y (theo phương X)
- My quay quanh trục X (theo phương Y)
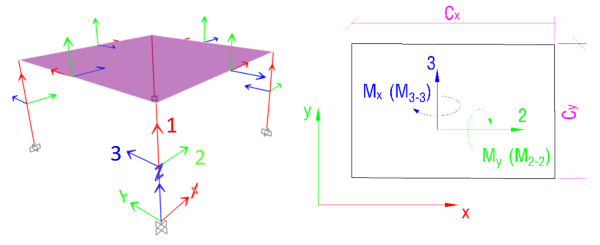
Quy ước phương chiều file tính Cemcons:
- Mx=M33: Moment quay quanh trục X hay tương đương quay quanh trục 3 trong ETABS
- My=M22: Mx: Moment quay quanh trục Y hay tương đương quay quanh trục 2 trong ETABS.
Do đó: Mx và My lấy đúng chiều quy ước so với ETABS để tính toán chính xác.
Điều kiện áp dụng: \(0.5 \leq \frac{C_x}{C_y} \leq 2\), cốt thép được đặt theo chu vi.
Tóm tắt giản đồ thiết kế:
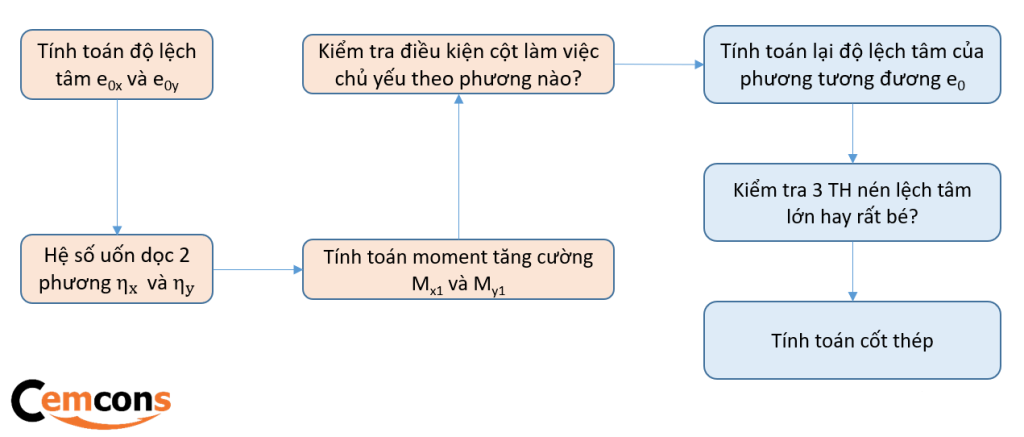
Tính chiều cao giới hạn vùng bê tông chịu nén: \(\xi_R = \frac{x_R}{h_0} = \frac{0.8}{1 + \frac{\varepsilon_{s,\text{el}}}{\varepsilon_{b2}}}\)
Độ lệch tâm ngẫu nhiên theo 2 phương: \(e_{ax} = \max\left(\frac{L}{600}, \frac{C_x}{30}, 10 \, \text{mm}\right) \quad \text{and} \quad e_{ay} = \max\left(\frac{L}{600}, \frac{C_y}{30}, 10 \, \text{mm}\right)\)
Tính độ mảnh theo 2 phương: \(\lambda_x = \frac{L_{ox}}{0.288 C_x}, \quad \lambda_y = \frac{L_{oy}}{0.288 C_y} \quad \Rightarrow \quad \lambda = \max(\lambda_x, \lambda_y)\)
Kết cấu siêu tĩnh:
\(e_{1x} = \frac{M_x}{N} \quad \Rightarrow \quad e_{ox} = \max(e_{1x}, e_{ax})\)
\(e_{1y} = \frac{M_y}{N} \quad \Rightarrow \quad e_{oy} = \max(e_{1y}, e_{ay})\)
Kết cấu tĩnh định:
\(e_{1x} = \frac{M_x}{N} \quad \Rightarrow \quad e_{ox} = e_{1x} + e_{ax}\)
\(e_{1y} = \frac{M_y}{N} \quad \Rightarrow \quad e_{oy} = e_{1y} + e_{ay}\)
Tính toán hệ số uốn dọc dựa theo giáo trình thầy Cống:
Nếu \(\lambda_x \leq 14 \quad \Rightarrow \quad \eta_x = 1\), ngược lại tính hx theo công thức:
\(I_x = \frac{C_y C_x^3}{12} \quad \Rightarrow \quad N_x^{cr} = \frac{2.5 E_b I_x}{L_{ox}^2} \quad \Rightarrow \quad \eta_x = \frac{1}{1 – \frac{N}{N_x^{cr}}}\)
Nếu \(\lambda_y \leq 14 \quad \Rightarrow \quad \eta_y = 1\), ngược lại tính hy theo công thức:
\(I_y = \frac{C_x C_y^3}{12} \quad \Rightarrow \quad N_y^{cr} = \frac{2.5 E_b I_y}{L_{oy}^2} \quad \Rightarrow \quad \eta_y = \frac{1}{1 – \frac{N}{N_y^{cr}}}\)
Ngoài ra lực tới hạn còn có thể tính toán theo các công thức thực nghiệm khác (trang 27, 28, 29):
\(N_{cr} = \frac{4800 R_b I}{L_o^2}\)
hoặc \(N_{cr} = \frac{C_s R_b A_b h^2}{L_0^2}\), với \(C_s = \frac{66000}{R + 350} = \left( \frac{1}{\frac{e_0}{h} + 0.16} + 200 \mu_s + 1 \right)\)
Tính toán lực tới hạn theo TCVN 5574-2018:
\(N_{cr} = \frac{\pi^2 D}{L_0^2}\)
\(D = k_b E_b I + k_s E_s I_s\)
D – độ cứng của cấu kiện BTCT ở trạng thái giới hạn về độ bền.
Eb, Es – mô đun đàn hồi lần lượt của bê tông và cốt thép.
I, Is – mô men quán tính của diện tích tiết diện lần lượt của bê tông và của toàn bộ cốt thép dọc đối với trọng tâm tiết diện ngang của cấu kiện.
kb, ks là các hệ số: ks = 0.7; kb được xác định theo công thức: \(k_b = \frac{0.15}{\phi_L (0.3 + \delta_e)}\)
\(\delta_e = \frac{e_0}{h}\) – độ lệch tâm tương đối của lực dọc: \(0.15 \leq \delta_e \leq 1.5\)
\(\phi_L\) – Hệ số xét đến ảnh hưởng của tải trọng: \(\phi_L = 1 + \frac{M_{L1}}{M_L} \leq 2\)
- ML là mô men đối với trọng tâm của thanh thép chịu kéo nhiều nhất hoặc chịu nén ít nhất (khi toàn bộ tiết diện chịu nén) do tác dụng của toàn bộ tải trọng.
- ML1 là mô men đối với trọng tâm của thanh thép chịu kéo nhiều nhất hoặc chịu nén ít nhất (khi toàn bộ tiết diện chịu nén) do tác dụng của TT thường xuyên và tạm thời dài hạn.
Momen gia tăng khi xét uốn dọc:
\(M_{x1} = \eta_x M_x; \quad M_{y1} = \eta_y M_y\)
Các trường hợp tính toán:
Mô hình | Theo phương X | Theo phương Y |
Điều kiện | \(\frac{M_{x1}}{C_x} > \frac{M_{y1}}{C_y}\) | \(\frac{M_{y1}}{C_y} > \frac{M_{x1}}{C_x}\) |
Các biểu thức tính toán | \(h = C_x; \quad b = C_y M_1 = M_{x1}; \quad M_2 = M_{y1} e_a = e_{ax} + 0.2 e_{ay}\) | \(h = C_y; \quad b = C_x M_1 = M_{y1}; \quad M_2 = M_{x1} e_a = e_{ay} + 0.2 e_{ax}\) |
Giả thiết: \(h_o = h – a; \quad z = h – 2a\)
Tính toán chiều cao vùng nén: \(x_1 = \frac{N}{R_b b}\)
Hệ số chuyển đổi mo :
\(x_1 \leq h_o \quad \Rightarrow \quad m_o = 1 – \frac{0.6x}{h_o}\)
\(x_1 > h_o \quad \Rightarrow \quad m_o = 0.4\)
Momen tương đương: \(M = M_1 + m_o \frac{M_2 h}{b}\)
Độ lệch tâm:
- Kết cấu tĩnh định: \(e_1 = \frac{M}{N} \quad \Rightarrow \quad e_o = e_1 + e_a\)
- Kết cấu siêu tĩnh: \(e_o = \max(e_1, e_a)\)
Khoảng cách từ điểm đặt lực đến trọng tâm cốt thép: \(e = e_o + 0.5h – a\)
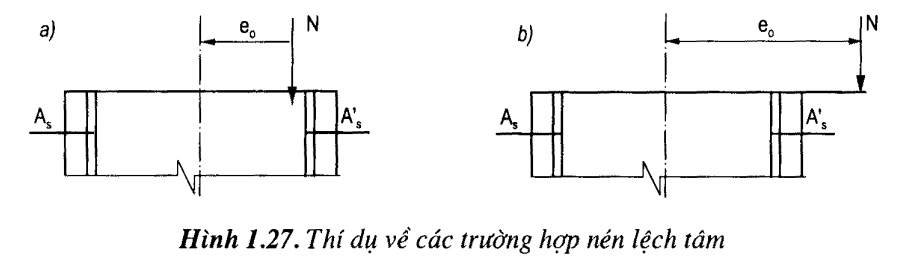
TH1: Nén lệch tâm rất bé: \(\epsilon = \frac{e_0}{h_0} \leq 0.3\)
TH2: Nén lệch tâm bé: \(\epsilon = \frac{e_0}{h_0} > 0.3, \quad x_1 > \xi_R \cdot h_0\)
TH3: Nén lệch tâm lớn: \(\epsilon = \frac{e_0}{h_0} > 0.3, \quad x_1 > \xi_R \cdot h_0\)
Trong đó: \(e_o = \max(e_1, e_a)\)
\(\xi_R = \frac{X_R}{h_0} = \frac{0.8}{1 + \frac{\epsilon_{s,el}}{\epsilon_{b2}}}\)
Nhắc lại lý thuyết SBVL:
- Trục trung hòa là trục chia ứng suất 2 phần của tiết diện thành 2 vùng kéo (+) và nén (-). Trên trục này ứng suất và biến dạng bằng 0.
- Vị trí trục trung hòa có thể di chuyển từ (+) vô cùng cho tới nằm trong tiết diện và di chuyển ra (-) vô cùng, tùy thuộc vào độ lớn, phương chiều, và điểm đặt của ngoại lực tác dụng.
Tính toán cốt thép
Trường hợp | NLT rất bé | NLT bé | NLT lớn |
Điều kiện | \(\epsilon = \frac{e_0}{h_0} \leq 0.3\) | \(\epsilon = \frac{e_0}{h_0} > 0.3, \quad x_1 > \xi_R \cdot h_0\) | \(\epsilon = \frac{e_0}{h_0} > 0.3, \quad x_1 \leq \xi_R \cdot h_0\) |
Các biểu thức tính toán | \(\gamma_e = \frac{1}{(0.5 – \epsilon)(2 + \epsilon)}, \quad \phi_e = \phi + \frac{(1 – \phi) \epsilon}{0.3}\) Trong đó: \(\lambda = \max(\lambda_x, \lambda_y)\) \(\lambda \leq 14 \Rightarrow \phi = 1\) \(14 < \lambda < 104 \Rightarrow \phi = 1.028 – 0.0000288 \lambda^2 – 0.0016 \lambda\) \(A_s \geq \frac{\gamma_e \cdot N}{\phi_e} – \frac{R_b \cdot b \cdot h}{R_{sc} – R_b}\) | \(x_1 = \left( \xi_R + \frac{1 – \xi_R}{1 + 50 \epsilon_0^2} \right) h_0\) \(\epsilon_0 = \frac{e_0}{h}\) \(A_s = \frac{N_e – R_b \cdot b \cdot x_1 \left( h_0 – \frac{x}{2} \right)}{0.4 \cdot R_{sc} \cdot Z}\) | \(A_s = \frac{N \left(e + 0.5 \cdot x_1 – h_0 \right)}{0.4 \cdot R_s \cdot Z}\) |
Giá trị Ast có thể dương hoặc âm. Nếu Ast <0 kích thước tiết diện cột quá lớn. Như vậy, lúc này có thể rút bớt tiết diện tính lại hoặc đặt cốt thép theo yêu cầu tối thiểu hoặc lấy bằng tầng trên vì thực tế cột được thi công từng tầng 1. Ngoài ra, kích thước cột còn bị khống chế bởi chuyển vị lệch tầng, chuyển vị đỉnh và chu kì.
Nếu Ast>0: \(\mu = \frac{A_{st}}{b \cdot h_0}\)
\(\mu < \mu_{\text{min}} = 0.5\% \Rightarrow A_{st} = \mu_{\text{min}} \cdot b \cdot h\) hoặc rút bớt tiết diện
\(\mu_{\text{min}} \leq \mu \leq \mu_{\text{max}} = 3\%\)
\(\mu > \mu_{\text{max}}\) Thép chịu lực lớn >> Tăng kích thước tiết diện cột.
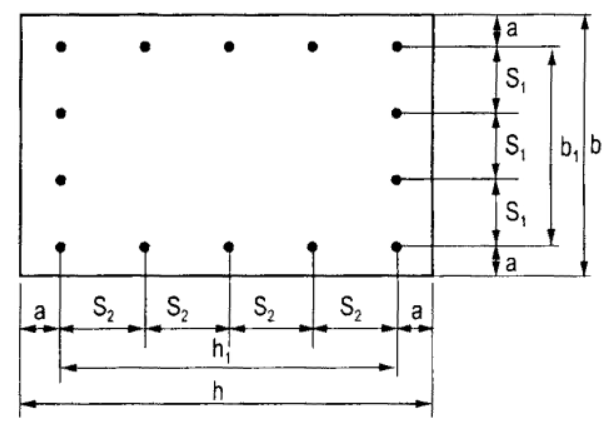
Khi cột chịu nén lệch tâm rất bé: Cốt thép đặt theo chu vi (mật độ cốt thép theo cạnh b có thể lớn hơn).
Khi cột chịu nén lệch tâm lớn: Cốt thép đặt theo chu vi trong đó mật độ cốt thép theo cạnh b lớn hơn hoặc bằng cạnh h).
Ví dụ tính toán
Các thông số: \(N = 91.94 \, \text{kN}, \quad M_y = 1.63 \, \text{kNm}, \quad M_x = 24.25 \, \text{kNm}\)
Bê tông B20: \(R_b = 11.5 \, \text{MPa}, \quad E_b = 27000 \, \text{MPa}\)
Cốt thép CII: \(R_s = R_{sc} = 280 \, \text{MPa}, \quad E_s = 21000 \, \text{MPa}\)
\(C_x = 250 \, \text{mm}, \quad C_y = 300 \, \text{mm}, \quad L = 3300 \, \text{mm}, \quad a = 40 \, \text{mm}, \quad \mu_{\text{max}} = 3\%, \quad \mu_{\text{min}} = 1\%\)
Bố trí cốt thép theo chu vi.
Lời giải chi tiết:
Kiểm tra điều kiện: \(0.5 \leq \frac{C_x}{C_y} = \frac{250}{300} = 0.84 \leq 2\)
Lấy: \(\xi_R = \frac{X_R}{h_0} = \frac{0.8}{1 + \frac{\varepsilon_{s,el}}{\varepsilon_{b2}}} = 0.579\)
\(\Psi = 0.7 \Rightarrow L_{ox} = L_{oy} = 0.7 \times 3300 = 2310 \, \text{mm}\)
Độ lệch tâm ngẫu nhiên theo hai phương:
\(e_{\text{ax}} = \max \left( \frac{L}{600}, \frac{C_x}{30}, 10 \, \text{mm} \right) = \max \left( \frac{3300}{600}, \frac{250}{30}, 10 \, \text{mm} \right) = 10 \, \text{mm}\)
\(e_{\text{ay}} = \max \left( \frac{L}{600}, \frac{C_y}{30}, 10 \, \text{mm} \right) = \max \left( \frac{3300}{600}, \frac{300}{30}, 10 \, \text{mm} \right) = 10 \, \text{mm}\)
Độ mảnh theo hai phương:
\(\lambda_x = \frac{L_x}{0.288 C_x} = \frac{2310}{0.288 \times 250} = 32\)
\(\lambda_y = \frac{L_y}{0.288 C_y} = \frac{2310}{0.288 \times 300} = 26.7\)
\(\Rightarrow \lambda = \max (\lambda_x, \lambda_y) = \max (32, 26.7) = 32\)
Kết cấu siêu tĩnh:
\(e_{1x} = \frac{M_x}{N} = \frac{24.95}{91.34} = 0.264 \, \text{m} = 264 \, \text{mm} \Rightarrow e_{ox} = \max(e_{1x}, e_{ax}) = \max(264, 10) = 264 \, \text{mm}\)
\(e_{1y} = \frac{M_y}{N} = \frac{1.63}{91.34} = 0.018 \, \text{m} = 18 \, \text{mm} \Rightarrow e_{oy} = \max(e_{1y}, e_{ay}) = \max(18, 10) = 18 \, \text{mm}\)
Xét uốn dọc:
\(\lambda_x = 32 > 14 \Rightarrow I_x = \frac{C_y C_x^3}{12} = \frac{300 \times 250^3}{12} = 390625000 \, \text{mm}^4\)
\(N_x^{\text{cr}} = \frac{2.5 \, E_b \, I_x}{L_{\text{ox}}^2} = \frac{2.5 \times 27000 \times 390625000}{2310^2} = 4941284 \, \text{N} \Rightarrow \eta_x = \frac{1}{1 – \frac{N}{N_x^{\text{cr}}}} = \frac{1}{1 – \frac{91940}{4941284}} = 1.019\)
\(\lambda_y = 26.7 > 14 \Rightarrow I_y = \frac{C_x C_y^3}{12} = \frac{250 \times 300^3}{12} = 562500000 \, \text{mm}^4\)
\(N_y^{\text{cr}} = \frac{2.5 \, E_b \, I_y}{L_{\text{oy}}^2} = \frac{2.5 \times 27000 \times 562500000}{2310^2} = 7115449.5 \, \text{N} \Rightarrow \eta_y = \frac{1}{1 – \frac{N}{N_y^{\text{cr}}}} = \frac{1}{1 – \frac{91940}{7115449.5}} = 1.013\)
Moment gia tăng khi xét uốn dọc:
\(M_x^* = \eta_x M_x = 1.013 \times 24.25 = 24.57 \, \text{kNm}\)
\(M_y^* = \eta_y M_y = 1.019 \times 1.63 = 1.66 \, \text{kNm}\)
Mô hình tính toán:
\(\frac{M_x^*}{C_x} = \frac{24.57 \times 1000}{250} = 98.28 \, \text{kN} > \frac{M_y^*}{C_y} = \frac{1.66 \times 1000}{300} = 5.5 \, \text{kN}\)
\(\Rightarrow h = C_x = 250 \, \text{mm}; \quad b = C_y = 300 \, \text{mm}\)
\(\Rightarrow M_1 = M_x^* = 24.57 \, \text{kNm}; \quad M_2 = M_y^* = 1.66 \, \text{kNm}\)
\(\Rightarrow e_a = e_{\text{ax}} + 0.2 \, e_{\text{ay}} = 10 + 0.2 \times 10 = 12 \, \text{mm}\)
\(a = 40 \, \text{mm} \Rightarrow h_o = h – a = 250 – 40 = 210 \, \text{mm}; \quad z = h – 2a = 250 – 2 \times 40 = 170 \, \text{mm}\)
\(x_1 = \frac{N}{R_b b} = \frac{91.94 \times 1000}{11.5 \times 300} = 26.6 \, \text{mm} \leq h_o = 210 \, \text{mm} \Rightarrow m_o = 1 – \frac{0.6 \times 26.6}{210} = 0.924\)
Moment tương đương:
\(M = M_1 + m_o M_2 \frac{h}{b} = 24.57 + 0.924 \times 1.65 \times \frac{250}{300} = 25.84 \, \text{kNm}\)
\(e_1 = \frac{M}{N} = \frac{25.84 \times 1000}{91.94} = 281 \, \text{mm}\)
\(\Rightarrow e_o = \max(e_1 + e_a) = 281 \, \text{mm}\)
\(\Rightarrow e = e_o + 0.5h – a = 281 + 0.5 \times 250 – 40 = 366 \, \text{mm}\)
Trường hợp tính toán
\(\varepsilon = \frac{e_o}{h_o} = \frac{281}{210} = 1.34 > 0.3\)
\(x = 26.6 \, \text{mm} < \xi_R h_o = 0.579 \times 210 = 121.66 \, \text{mm}\)
⇒ TH3: Lệch tâm lớn
Diện tích cốt thép
Với k=0.4
\(A_{st} = \frac{N(e + 0.5x_1 – h_o)}{k R_s z} = \frac{91.94 \times 1000 (366 + 0.5 \times 26.6 – 210)}{0.4 \times 280 \times 170} = 817 \, \text{mm}^2\)
Đánh giá và xử lý kết quả
\(\mu_{\text{min}} = 0.5\% \leq \mu = \frac{A_{\text{st}} \times 100}{b h_o} = \frac{817 \times 100}{300 \times 210} = 1.3\% \leq \mu_{\text{max}} = 3\%\)
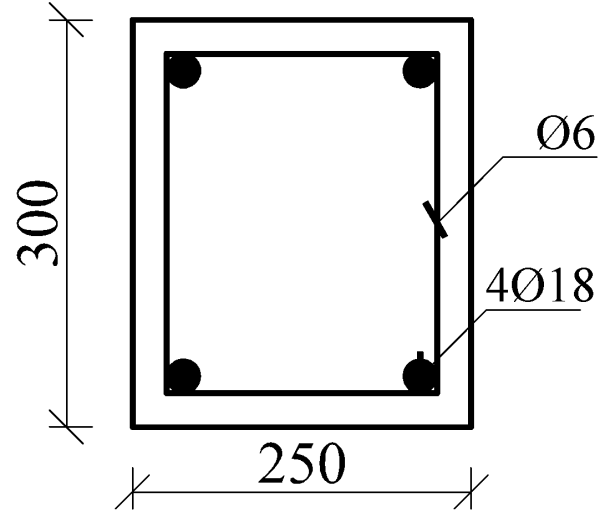
Bố trí cốt thép: Chọn 4Φ18 bố trí 4 góc
\(A_c = \frac{4\pi d^2}{4} = 4\pi \left(\frac{18^2}{4}\right) = 1018 \, \text{mm}^2\)
Tài liệu tham khảo
- Tiêu chuẩn TCVN 2737-2023
- Tiêu chuẩn TCVN 5574-2018
- Tiêu chuẩn Eurocode 2
- Thiết kế bê tông cốt thép theo TCVN 5574-2018, thầy Bùi Quốc Bảo
- Hướng dẫn tính toán cấu kiện bê tông cốt thép theo tiêu chuẩn TCVN 5574-2018, cô Đoàn Thị Quỳnh Mai và cộng sự
- “Tính toán tiết diện cột bê tông cốt thép” của thầy Nguyễn Đình Cống
Link Cemapp Tính toán và thiết kế cột BTCT hàng loạt theo TCVN 5574:2018
Bạn đọc tham khảo khóa học Hướng dẫn đồ án tốt nghiệp thiết kế nhà cao tầng theo TCVN mới nhất
Khóa học Hướng dẫn đồ án tốt nghiệp ngành Xây dựng theo tiêu chuẩn Eurocodes
Like và share nếu thấy bổ ích <3
Bài viết gần đây


AutoCAD hay Revit – Đâu là lựa chọn tối ưu cho dân xây dựng thời 4.0?


Tài liệu chuyên ngành kĩ thuật Xây Dựng ĐH Bách Khoa TP.HCM




2 bình luận về “Tính toán cột chịu nén lệch tâm xiên”
thầy ơi cho em hỏi với ạ ở trường hợp cột lệch tâm xiên em thấy có nói về góc nghiêng của mặt phẳng uốn so với trục là φ₀ , mà trong tính toán theo phương pháp quy về lệch tâm phẳng tương đương thì không thấy sự tham gia hay xuất hiện của hệ số này ạ , theo em hiểu tan(φ)=Mx/My , hay Mtd=(Mx^2+My^2)^1/2
hi em,
Đúng là nó sẽ có cái góc phi đó. Nhưng theo phương pháp này thì mình sẽ quy từ lệch tâm xiên về lệch tâm phẳng nhé em.
Lúc này góc nghiêng đó đã được bù đắp bằng hệ số khuếch đại moment rồi em nhé.