Tính toán tải trọng gió theo TCVN 2737:2023

Mở đầu

Các tòa nhà cao tầng, cầu vượt, và các công trình công nghiệp luôn phải đối mặt với sức gió mạnh. Để đảm bảo an toàn cho công trình và người sử dụng, việc tính toán chính xác tải trọng gió là vô cùng quan trọng. Ngoài ra, tình hình biến đổi khí hậu tại Việt Nam diễn biến ngày càng khó lường với các trận bão ngày càng thường xuyên với vận tốc gió lớn.

Tiêu chuẩn TCVN 2737-2023 được ra đời vào năm 2023 rất cấp thiết và kịp thời nhằm cung cấp một hướng dẫn chi tiết để thực hiện quá trình tính toán này, giúp các kỹ sư thiết kế có thể đưa ra những quyết định thiết kế an toàn và tối ưu hơn.

Trong bài viết này, Cemcons sẽ đưa ra quy trình tính toán tải trọng gió theo TCVN 2737-2023 và cùng với đó là những lưu ý quan trọng trong quá trình tính toán.

Công thức tính toán

Giá trị tiêu chuẩn của tải trong gió (W_k) được xác định theo công thức:

\(W_k=W_{(3s,10)}×k(z_e)×c×G_f\) (1)

Trong đó:

\(W_{(3s,10)}\) – áp lực gió 3s ứng với chu kỳ lặp 10 năm.
\(k(z_e)\)- hệ số kể đến sự thay đổi áp lực gió theo độ cao và dạng địa hình tại độ cao tương đương \(k(z_e)\).
\(c\) – hệ số khí động.
\(G_f\) – hệ số hiệu ứng giật.

Điều này áp dụng cho công trình có chiều cao không lớn hơn 200 m hoặc nhịp không lớn hơn 150 m.

1. \(W_{(3s,10)}\) - áp lực gió 3s ứng với chu kỳ lặp 10 năm

Được xác định theo công thức (2):

\(W_{(3s,10)}=γ_t×W_0\) (2)

Trong đó:

\(γ_t= 0.852\) hệ số chuyển đổi áp lực gió từ chu kỳ lặp từ 20 năm xuống 10 năm.
\(W_{(3s,10)}\) (daN/m²) – áp lực gió cơ sở theo bảng 1 được xác định theo mục 5.2, trong QC 02:2022-BXD.

Bảng 1 – Giá trị cơ sở \(W_0\) theo bảng đồ phân vùng áp lực gió trên lãnh thổ Việt Nam

Vùng áp lực gió trên bản đồ	I	II	III	IV	V
\(W_0\) (daN/m²)	65	95	125	155	185

Đối với các công trình xây dựng ở những vùng có địa hình phức tạp, giá trị áp lực gió cơ sở \(W_0\) được xác định theo công thức (3):

\(W_0=0.0613xV_0^2\) (3)

\(V_0\) – vận tốc gió cơ sở, được lấy trung bình trong khoảng thời gian 3s, chu kỳ lặp 20 năm, ở độ cao 10m so với mốc chuẩn, tương ứng với địa hình dạng B.

2. \(k(z_e)\) - hệ số kể đến sự thay đổi áp lực gió theo độ cao và dạng địa hình tại độ cao tương đương \(z_e\)

Được xác định theo công thức (4):

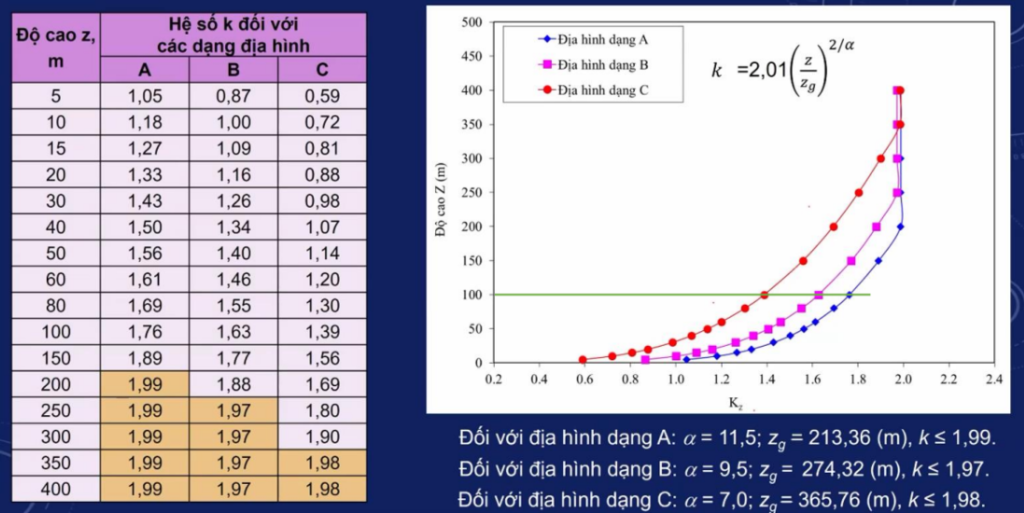
\(k(z_e)=2.01×(z_e/z_g )^{(2/α)}\) (4)

Trong đó:

\(z_e\) – độ cao tương đương, lấy không nhỏ hơn \(z_{min}\).
\(z_g\) – độ cao gadient.
α – hệ số dùng trong hàm lũy thừa đối với vận tốc gió 3s.

Lưu ý: Giá trị hệ số \(k(z_e)\) lấy không lớn hơn 1.99; 1.97 và 1.98 lần lượt đối với các dạng địa hình A, B, C.

2.1 \(z_e\)

Được xác định như sau:

a) Đối với tháp, trụ, ống, kết cấu rỗng và tương tự: \(z_e=z\);

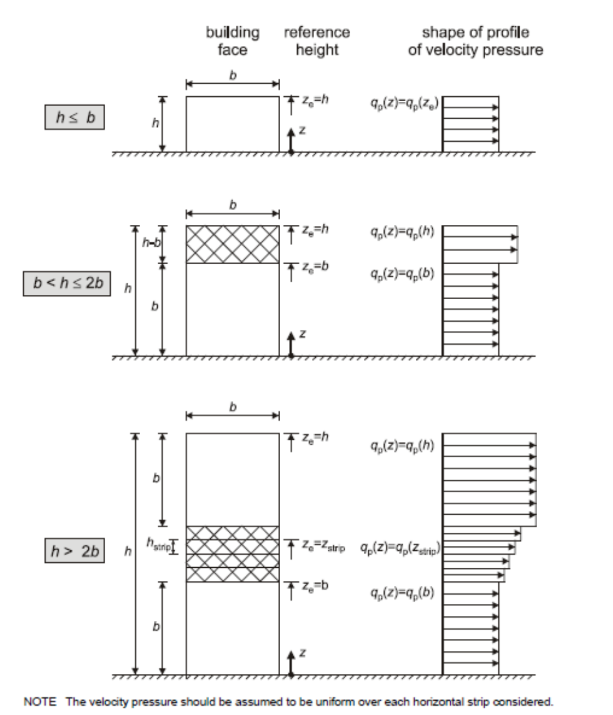
b) Đối với nhà:

1) Khi \(h≤b: z_e=h\).

2) Khi \(b<h≤2b\):

\(z>b\) thì \(z_e=h)\
\(0<z≤b\) thì \(z_e=b\)

3) Khi \(h>2b\):

\(z≥h–b\) thì \(z_e\)=h\)
\(b<z<h–b\) thì \(z_e=z\)
\(0<z≤b\) thì \(z_e=b\)

Trong đó:

z – độ cao so với mặt đất;
b – chiều rộng của nhà (không kể khối
đế), vuông góc với hướng gió;
h – chiều cao của nhà.

2.2 \(z_g,z_{min},α\)

Bảng 2 – Các hệ số \(z_g,z_{min},α\)

Dạng địa hình	Giá trị \(z_g\), m	Giá trị \(z_{min}\), m	Giá trị \(α\)
A (Trống trải)	213.36	2.13	11.5
B (Ít trống trải)	274.32	4.57	9.5
C (Bị che chắn)	365.76	9.14	7.0

Bảng 3 – Hệ số k(z_e) (Mục 10.2.5 bảng 9 TCVN 2737:2023)

3. c - hệ số khí động

c là hệ số khí động được quy định tại phụ lục F, tùy theo từng dạng công trình trong đó dấu “cộng” của các hệ số c_e và c_i ứng với hướng áp lực gió vào bề mặt tương ứng, dấu “trừ” ứng với hướng ra ngoài bề mặt tương ứng.

Đối với các công trình đều đặn có mặt bằng hình chữ nhật hoặc tương đương (Chiếm 70%, 80% công trình dân dụng), ta có thể dùng phụ lục:

F.4 (chỉ khi \(h/d≤5\)-ưu tiên sử dụng)
F.16 (khi \(h/d≤5\) hoặc \(h/d>5\))

3.1. Theo phụ lục F4

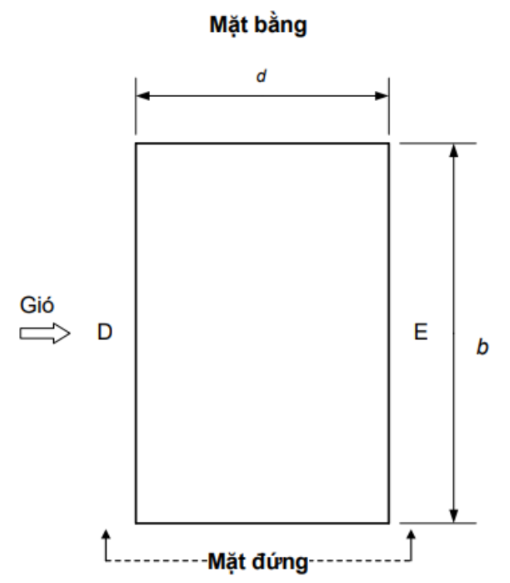
Hệ số khí động \(c_e\) cho các vùng trên các tường của nhà có mặt bằng chữ nhật (Hình F.5a) lấy theo Bảng F.4.

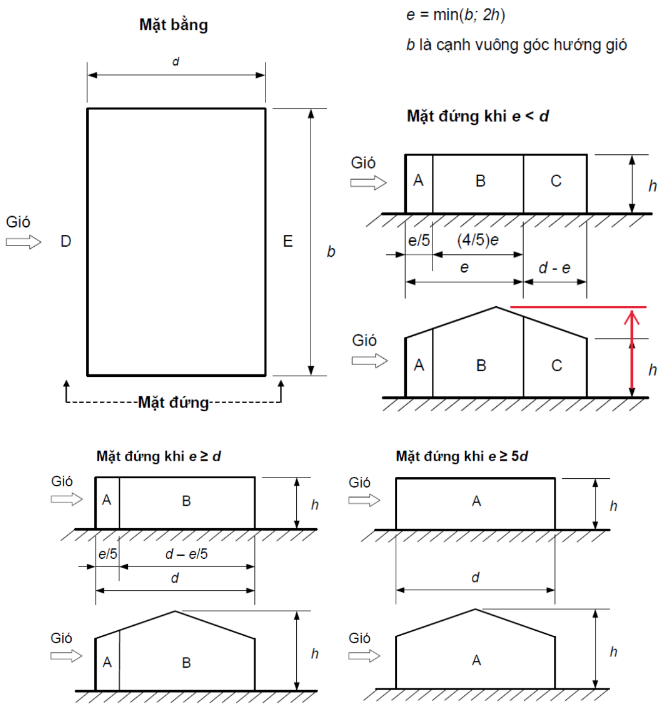
Hình F.5a – Tường thẳng đứng của nhà có mặt bằng chữ nhật

Bảng F.4 – Hệ số c_e cho tường thẳng đứng của nhà có mặt bằng chữ nhật

\(h/d\)	Vùng
\(h/d\)	A	B	C	D	E
5	-1.2	-0.8	-0.5	+0.8	-0.7
1	-1.2	-0.8	-0.5	+0.8	-0.5
≤ 0.25	-1.2	-0.8	-0.5	+0.7	-0.3

Lưu ý: các công trình bê tông cốt thép đều đặn, nếu gán gió vuông góc 90 độ vào bề mặt công trình thì chỉ quan tâm tới vùng gió D và E, vì các vùng khác gió sẽ tự triệu tiêu lẫn nhau do 2 hướng gió ngược nhau.

3.2. Theo phụ lục F.16

c là hệ số khí động được xác định theo công thức:

\(c_x=k_λ×c_{x∞}\) (5)

Trong đó:

\(k_λ\) – hệ số phụ thuộc vào độ mảnh hiệu dụng của công trình \(λ_e\).
\(c_{x∞}\) – hệ số khí động cho tiết diện n góc và các cấu kiện kết cấu.

Lưu ý: Cách xác định hệ số khí động này áp dụng cho công trình lăng trụ, tiết diện chữ nhật, hệ số đặc có thể lấy bằng ϕ=1 khi kể đến trường hợp nguy hiểm nhất.

3.2.1. \(k_λ\) – hệ số phụ thuộc vào độ mảnh hiệu dụng của công trình \(λ_e\).

Được lấy theo hình F.27 phụ lục F.18:

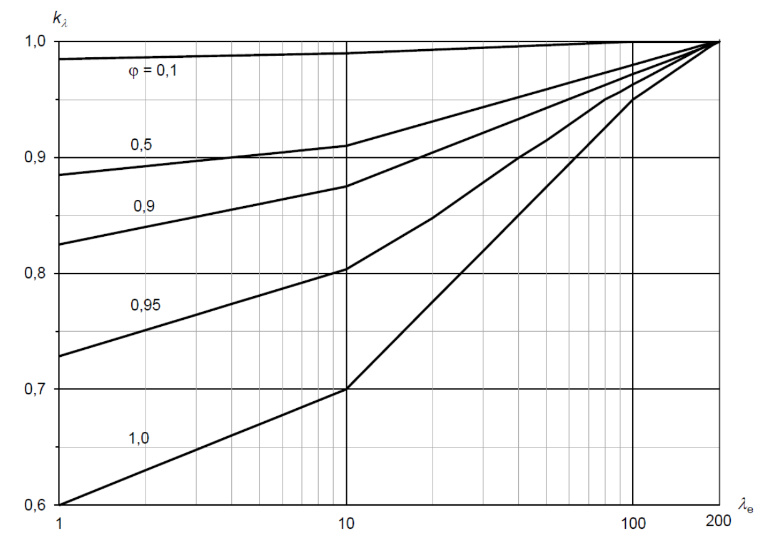
Hình F.27 – Hệ số \(k_λ\)

Theo phụ lục F.18:

\(λ_e\) – Độ mảnh hiệu dụng : phụ thuộc vào độ mảnh \(λ=L/b\): được xác định theo bảng F.15 :

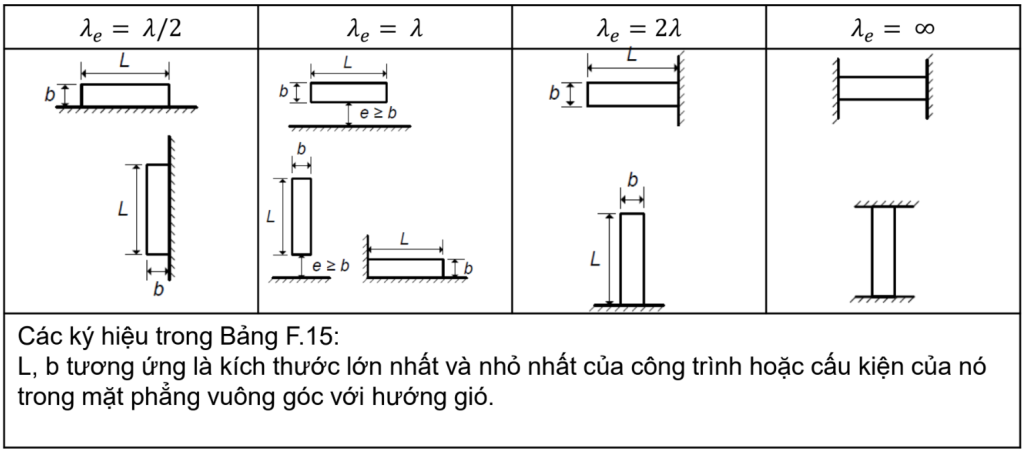
Bảng F.15 – Độ mảnh hiệu dụng \(λ_e\)

Lưu ý: Ta có thể xác định \(k_λ\)dựa trên các phương trình sau:

\(k_λ=0.1×log⁡λ_e+0.6 (1≤λ_e≤10)\)
\(k_λ=0.25×logλ_e+0.45 (10≤λ_e≤100)\)
\(k_λ=0.1661×log λ_e+0.6178 (100≤λ_e≤200)\)

3.2.2. \(c_{x∞}\) – hệ số khí động cho tiết diện n góc và các cấu kiện kết cấu

Được lấy theo hình F.22 đối với tiết diện chữ nhật:

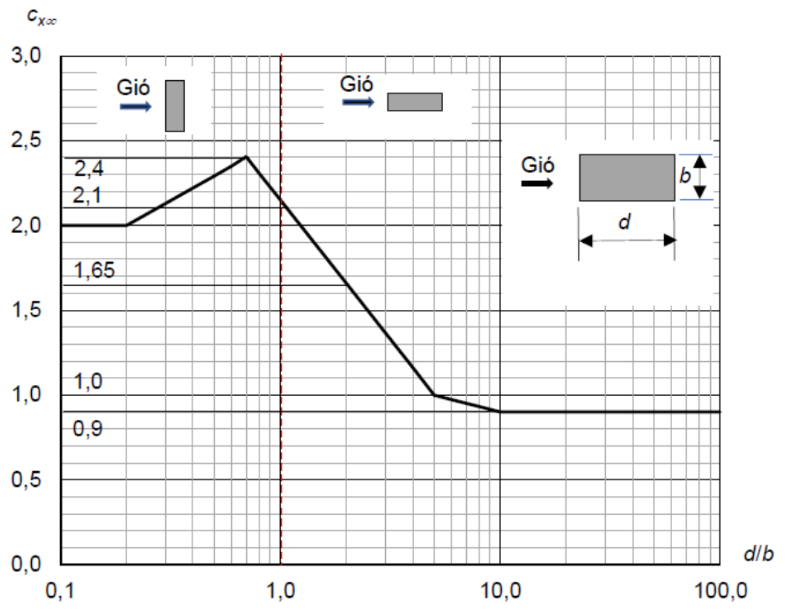
Hình F.22 – Hệ số đối với công trình tiết diện chữ nhật \(c_{x∞}\)

Lưu ý: Ta có thể xác định \(c_{x∞}\)dựa trên các phương trình sau:

\(c_x∞=2 (0.1<d⁄b≤0.2)\)
\(c_x∞=0.735×log⁡(d⁄b)+2.514 (0.1<d⁄b≤0.7)\)
\(c_x∞=-1.640×log⁡(d⁄b)+2.146 (0.7<d⁄b≤5)\)
\(c_x∞=-0.332×log⁡(d⁄b)+1.232 (5<d⁄b≤10)\)
\(c_x∞=0.9 (10<d⁄b≤100)\)

Theo phụ lục F.16:

Hệ số \(c_{x∞}\) đối với tiết diện n góc và các cấu kiện kết cấu (dạng địa hình), được xác định theo bảng F.12:

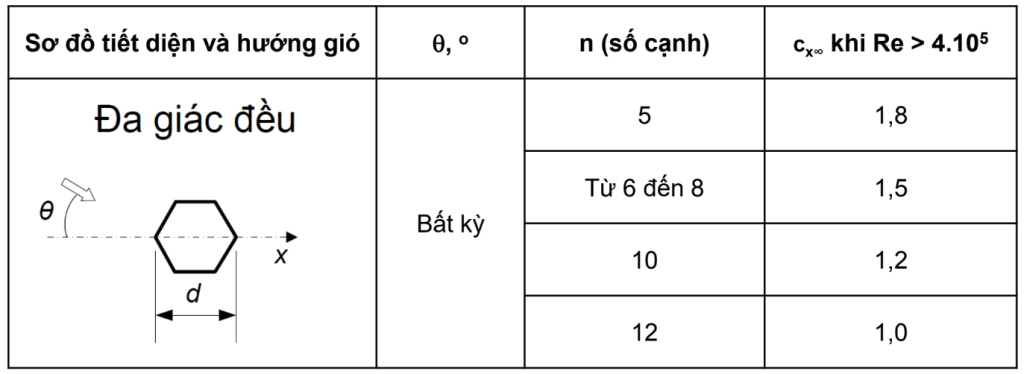
Bảng F.12 – Hệ số \(c_{x∞}\) cho tiết diện n góc và các cấu kiện kết cấu (dạng địa hình)

4. \(G_f\) - hệ số hiệu ứng giật

Cách 1: Dùng công thức đơn giản

Đối với nhà bê tông cốt thép: \(G_f=0.85+\frac{h}{2840}\) (6)

Đối với nhà thép: \(G_f=0.85+\frac{h}{1010}\) (7)

Trong đó: h – chiều cao công trình tính bằng mét (m)

Lưu ý: Công thức trên dùng để tính toán sơ bộ hệ số \(G_f\) đối với nhà cao tầng có hình dạng đều đặn theo chiều cao và có chu kỳ dao động riêng cơ bản thứ nhất \(T_1>1s\) và chiều cao không quá 150 m.

Đối với kết cấu “cứng” (có chu kỳ dao động riêng cơ bản thứ nhất \(T_1≤1s\)) thì Gf có thể lấy bằng 0.85.

Cách 2: Dùng công thức tổng quan

Cách này khuyến nghị nên sử dụng để đảm bảo chính xác khi có xét đến các yếu tố khác của công trình như kích thước và động lực học của công trình.

Đối với kết cấu “mềm” (có chu kỳ dao động riêng cơ bản thứ nhất \(T_1>1s\)) được xác định theo công thức:

\(G_f=0.925\frac{1+1.7I(z_s)\sqrt{g_Q^2 Q^2+g_R^2 R^2 }}{1+1.7g_v I(z_s))}\) (8)

\(I(z_s)\) – độ rối ở độ cao tương đương \(z_s\), được xác định theo công thức:

\(I(z_s )=c_r(\frac{10}{z_s} )^{\frac{1}{6}}\) (9)

Trong đó:

\(c_r\) là hệ số, phụ thuộc vào các dạng địa hình khác nhau, lấy theo Bảng 10 (Giá trị các hệ số cho các dạng địa hình).

Dạng địa hình	\(c_r\)	\(l\),m	⋶	\(\overline{b}\)	\(\overline{α}\)
A	0.15	198.12	1/8	0.80	1/9
B	0.20	152.40	1/5	0.65	1/6.5
C	0.30	97.54	1/3	0.45	1/4

Bảng 10 – Giá trị các hệ số cho các dạng địa hình

\(z_s\) là độ cao tương đương của công trình, lấy bằng 0.6h, h là chiều cao của công trình.

\(g_Q\) là hệ số đỉnh cho thành phần xung của gió, lấy bằng 3.4;

\(g_v\) là hệ số đỉnh cho thành phần phản ứng của gió, lấy bằng 3.4;

\(g_R\) là hệ số đỉnh cho thành phần cộng hưởng của gió, được xác định theo công thức:

\(g_R=\sqrt{2ln⁡(3600n_1)}+\frac{0.577}{\sqrt{2ln⁡(3600n_1)}}\) (10)

Với: \(n_1\) là tần số dao động riêng cơ bản thứ nhất, để an toàn, lấy 2 phương X và Y bằng nhau và lấy trong mode 1 của mô hình ETABS.

Q là hệ số kể đến thành phần phản ứng nền của kết cấu chịu tải trọng gió, được xác định theo công thức:

\(Q=\frac{1}{1+0.63(\frac{(b+h)}{L(z_s)})^0.63}\) (11)

Với:

b là chiều rộng công trình, vuông góc với hướng gió tác dụng; h là chiều cao công trình.
L(z_s) là thang nguyên kích thước xoáy (chiều dài rối) tại độ cao tương đương theo công thức:
- \(L(z_s )=𝓁(\frac{z_s}{10})^⋶\) (12)
- Với: 𝓁 và ⋶ là các hệ số, phụ thuộc vào các dạng địa hình khác nhau, lấy theo bảng 10. \(z_s=0.6h\) là độ cao tương đương.

R là hệ số phản ứng cộng hưởng được xác định theo công thức:

\(R=\sqrt{\frac{1}{β}R_nR_hR_b(0.53+047R_d)}\) (13)

Trong đó:

β là độ cản, lấy bằng:
- 0.01 – cho kết cấu thép;
- 0.015 – cho kết cấu thép – bê tông;
- 0.02 – cho kết cấu bê tông và bê tông cốt thép.
\(R_n\) được xác định theo công thức:
- \(R_n=\frac{7.47N_1}{(1+10.3N_1)^{\frac{5}{3}}}\) (14)
- Với: \(N_1=\frac{n_1L(z_s)}{V(z_s)_{3 600s,50}}\) (15)
- \(V(z_s)_{3 600s,50}\) là vận tốc gió trung bình trong khoảng thời gian 3600 giây ứng với chu kỳ lặp 50 năm, tại độ cao tương đương zs, được xác định theo công thức:
  - \(V(z_s)_{3 600s,50}=\overline{b}(z_s/10)^\overline{α}V_{3s,50}\) (16)
  - \(V_{3s,50}\) là vận tốc gió 3s (lấy trung bình trong khoảng thời gian 3s) ứng với chu kỳ lặp 50 năm theo QCVN 02:2022.
  - Giá trị các hệ số \(\overline{b}\) và \(\overline{α}\) lấy theo bảng 10 phụ thuộc vào các dạng địa hình khác nhau.

\(R_h\), \(R_b\), \(R_d\) là các hàm số dẫn suất khí động, được xác định theo công thức:

\(R_h=\frac{1}{η_h}-\frac{1}{2η_h^2}(1-e^{-2η_h})\); \(R_h=1\) khi \(η_h=0\) (17)

\(R_b=\frac{1}{η_b}-\frac{1}{2η_b^2}(1-e^{-2η_b})\); \(R_b=1\) khi \(η_b=0\) (18)

\(R_d=\frac{1}{η_d}-\frac{1}{2η_d^2}(1-e^{-2η_d})\); \(R_d=1\) khi \(η_d=0\) (19)

Với:

\(η_h=4.6\frac{n_1h}{V(z_s)_{3 600s,50}} ; η_b=4.6\frac{n_1b}{V(z_s)_{3 600s,50}} ; η_d=4.6\frac{n_1d}{V(z_s)_{3 600s,50}}\) (20)
h, b và d lần lượt là chiều cao, chiều rộng và chiều sâu (hoặc chiều dài) của công trình.

Lưu ý khi tính toán diện tích truyền tải trọng gió cho mỗi tầng

Khi tính toán diện tích của các tầng chịu ảnh hưởng bởi tải trọng gió, ta sẽ tùy vào hình dạng của bề mặt để có công thức tính diện tích chính xác.

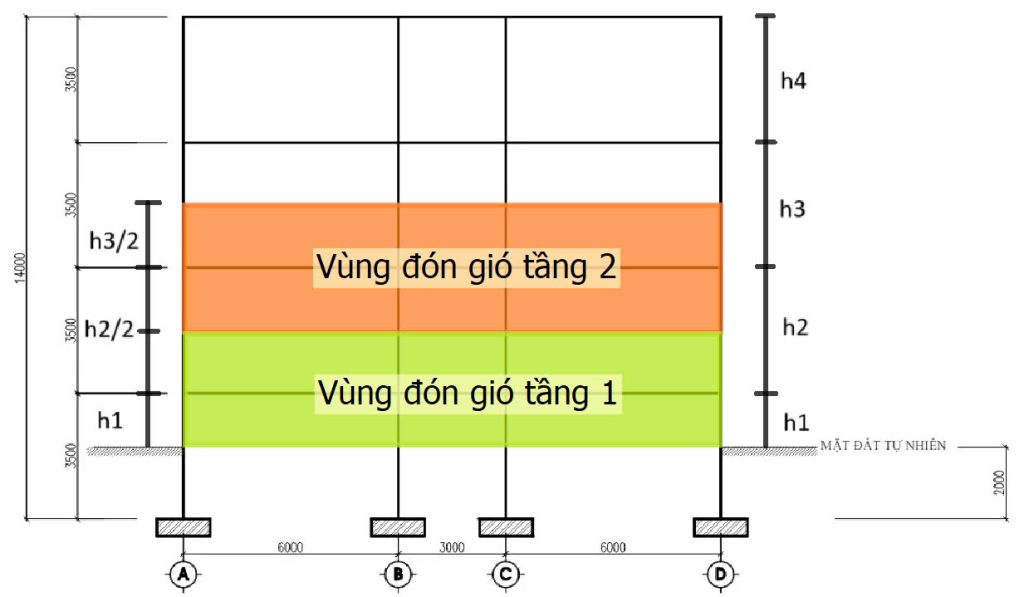
Ta xét công trình có hình dạng chữ nhật đơn giản trên làm ví dụ minh họa:

Đối với tầng 2 trở lên, ví dụ để tính toán diện tích truyền tải gió tầng 2, ta sẽ có công thức tính \(S=\frac{h_2+h_3}{2}\) với \(h_2\) và \(h_3\) lần lượt là chiều cao của tầng 2 và tầng 3, b là bề rộng đón gió của tầng đó. Tương tự cho các tầng trên còn lại. Lưu ý tầng mái nếu có lan can bảo vệ, phải kể diện tích chắn gió này.
Đối với tầng 1 có 2 cách: Cách 1 làm tương tự như trên, lấy một nửa tầng 2 và tầng 1 cộng lại. Cách 2 thiên về an toàn: Lấy một nửa tầng 2 và cộng hết chiều cao tầng 1.

Lưu ý khi gán tải gió vào ETABS

Lưu ý 1. Gán tải gió vào tâm nào của công trình?

Ở tiêu chuẩn TCVN 2737:2023, tải trọng gió gán vào tâm hình học (Center of Geometry) bởi vì lúc này gió được coi là gió tĩnh hoàn toàn (phần động được chuyển thành tĩnh bởi các hệ số giật G_f).

Điều này khác với tiêu chuẩn cũ TCVN 2737 :1995, chúng ta thường gán tải trọng gió động vào tâm khối lượng (Center of Mass) và tải trọng gió tĩnh gán vào tâm hình học (Center of Geometry).

Lưu ý 2. Cách gán tải gió bằng ETABS

Ta cần khai báo Rigid diaphragm để ETABS xác định tâm hình học cho sàn để chúng ta có thể gán tải gió vào tâm này của công trình.

Ngoài ra, bạn có thể tham khảo video hướng dẫn trên youtube của Cemcons Tính toán gió tự động theo TCVN 2737-2023 bằng ETABS V22 để biết cách khai báo chi tiết khi gán tải trọng gió vào mô hình ETABS.

Bài toán minh họa

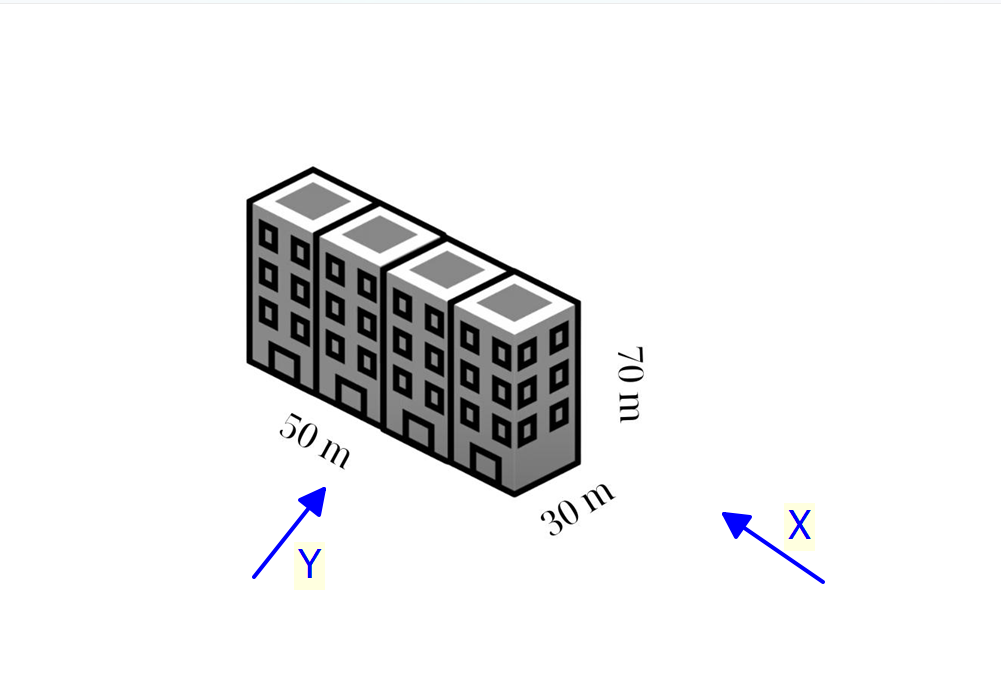
Tính tải trọng gió tác dụng vào công trình theo hai phương X, Y. Biết:

Công trình bao gồm 17 tầng: chiều cao tầng 1 là 6m, chiều cao tầng điển hình 4m.
Công trình được xây dựng tại Thành phố HCM, địa hình dạng B, khu vực II
Tổng chiều cao công trình 70m.
Kích thước mặt bằng công trình: 30×50 m.

Giá trị tiêu chuẩn của tải trọng gió (W_k):

\(W_k=W_{(3s,10)}×k(z_e)×c×G_f\)

Giá trị áp lực gió 3s ứng với chu kỳ lặp 10 năm (\(W_{(3s,10)}\)):

\(W_{(3s,10)}=γ_t×W_0\)

Với:

\(γ_t=0.852\)
Áp lực gió cơ sở theo khu vực II: \(W_0=95\) (daN/m²)

Suy ra: \(W_{(3s,10)}=0.852×95=80.94\) (daN/m²)

Tính toán giá trị của hệ số \(k(z_e)\) cho tầng 1:

Công thức: \(k(z_e)=2.01×(z_e/z_g )^{(2/α)}\)

a) Xác định giá trị \(z_e\):

Theo phương X:

Vì \(0<z_1=6m≤b_x=30m\) nên \(z_{ex}=b=30 \text{m}\).

Theo phương Y:

Vì \(0<z_2=6m≤b_y=50m\) nên \(z_{ey}=b=50 \text{m}\).

b) Xác định giá trị z_g, z_min và α:

Khu vực thuộc dạng địa hình B nên:

\(z_g=274.32 \text{m}\)
\(z_{min}=4.57 \text{m}\)
\(α=9.5\)

Giá trị của hệ số \(k(z_e)\) của tầng 1:

Theo phương X:

\(k(z_e)_x=2.01x(\frac{30}{274.32})^{2/9.5}=1.26\)

Theo phương Y:

\(k(z_e)_y=2.01x(\frac{50}{274.32})^{2/9.5}=1.40\)

Xác định hệ số khí động c theo phụ lục F.4:

Vùng	Phương X		Phương Y
Vùng	h/d=	1.400	h/d=	2.333
A	-1.20	6.0m	-1.20	10.0m
B	-0.80	24.0m	-0.80	20.0m
C	-0.50	20.0m	0.00	0.0m
D	0.800	30.0m	0.800	50.0m
E	-0.520	30.0m	-0.567	50.0m

Hệ số	Phương X	Phương Y
Hệ số khí động c	1.320	1.367

Hệ số hiệu ứng giật (\(G_f\)) đối với công trình bê tông cốt thép theo công thức đơn giản:

\(G_f=0.85+\frac{h}{2840}=0.85+\frac{70}{2840}=0.8746\)

Giá trị tiêu chuẩn của tải trọng gió:

Theo phương X:

\(W_{k-x}=W_{3s,10}×k(z_e)_x×c_x×G_f=80.94×1.26×1.32×0.8746=117.74 (\text{daN/m}^2)\)

Theo phương Y:

\(W_{k-y}=W_{3s,10}×k(z_e)_y×c_y×G_f=80.94×1.40×1.367×0.8746=135.48 (\text{daN/m}^2)\)

Tính toán giá trị áp lực gió tiêu chuẩn (\(W_{tc}\)) tầng 1:

Diện tích đón gió tầng 1:
- Theo phương X: \(S_{1X}=\frac{(h_1+h_2)}{2} \times b_{1X}=\frac{(6+4)}{2} \times 30 =150 \text{m}^2\)
- Theo phương Y: \(S_{1Y}=\frac{(h_1+h_2)}{2} \times b_{1Y}=\frac{(6+4)}{2} \times 50 =250 \text{m}^2\)
Giá trị áp lực gió tiêu chuẩn tầng 1:
- Theo phương X: \(W_{tcX} =S_{1X} \times W_{kX}=150 \times 117.74 \times 10^{-2} =176.61 \text{kN}\)
- Theo phương Y: \(W_{tcY} = S_{1Y} \times W_{kY}= 250 \times 135.48 \times 10^{-2} =338.7 \text{kN}\)

Với hệ số độ tin cậy của tải trọng gió: ɣ = 2.10 (TCVN 2737:2023)

Theo phương X: \(W_{ttX} = \gamma\times W_{tcX}=2.1 \times 176.61 =370.88 \text{kN}\)
Theo phương Y: \(W_{ttY} = \gamma \times W_{tcY}=2.1 \times 338.7 =711.27 \text{kN}\)

Tính toán tương tự cho các tầng còn lại ta được bảng tính toán sau (tính bằng phần mềm Cemapp):

Tên tầng	Chiều cao tầng (m)	Cao độ các tầng (m)	Bề rộng đón gió phương X (m)	Bề rộng đón gió phương Y (m)	Độ cao tương đương theo phương X (m)	Độ cao tương đương theo phương Y (m)	Hệ số k(ze) theo phương X	Hệ số k(ze) theo phương Y	Chiều cao đón gió (m)	Áp lực gió tiêu chuẩn theo phương X (kN)	Áp lực gió tiêu chuẩn theo phương Y (kN)	Áp lực gió tính toán theo phương X (kN)	Áp lực gió tính toán theo phương Y (kN)
Tầng 17	4	70	30	50	70	70	1.51	1.51	2	84.54	145.87	177.53	306.34
Tầng 16	4	66	30	50	70	70	1.51	1.51	4	169.07	291.75	355.05	612.67
Tầng 15	4	62	30	50	70	70	1.51	1.51	4	169.07	291.75	355.05	612.67
Tầng 14	4	58	30	50	70	70	1.51	1.51	4	169.07	291.75	355.05	612.67
Tầng 13	4	54	30	50	70	70	1.51	1.51	4	169.07	291.75	355.05	612.67
Tầng 12	4	50	30	50	70	50	1.51	1.4	4	169.07	271.8	355.05	570.77
Tầng 11	4	46	30	50	70	50	1.51	1.4	4	169.07	271.8	355.05	570.77
Tầng 10	4	42	30	50	70	50	1.51	1.4	4	169.07	271.8	355.05	570.77
Tầng 9	4	38	30	50	38	50	1.33	1.4	4	148.67	271.8	312.2	570.77
Tầng 8	4	34	30	50	34	50	1.3	1.4	4	145.23	271.8	304.98	570.77
Tầng 7	4	30	30	50	30	50	1.26	1.4	4	141.45	271.8	297.05	570.77
Tầng 6	4	26	30	50	30	50	1.26	1.4	4	141.45	271.8	297.05	570.77
Tầng 5	4	22	30	50	30	50	1.26	1.4	4	141.45	271.8	297.05	570.77
Tầng 4	4	18	30	50	30	50	1.26	1.4	4	141.45	271.8	297.05	570.77
Tầng 3	4	14	30	50	30	50	1.26	1.4	4	141.45	271.8	297.05	570.77
Tầng 2	4	10	30	50	30	50	1.26	1.4	4	141.45	271.8	297.05	570.77
Tầng 1	6	6	30	50	30	50	1.26	1.4	5	176.81	339.75	371.31	713.47